机器学习 · 总览篇 III - 蔡康的博客

统计推断作为重要的机器学习基础，对它的了解十分必要，否则我们做机器学习只是在黑盒操作，对其原理和结果难以解释

本文首发于我的知乎专栏《机器怎么学习》中机器学习·总览篇(3) 统计推断: 频率学派和贝叶斯学派，转载请保留链接 ;)

一、机器学习和统计推断的关系

这一小节谈到的机器学习是狭义上的概念，特指归纳学习，也是现在通常意义上的机器学习.

机器学习领域中的一个方向是通过统计推断中的『数值优化』来解决问题，称为统计学习
机器学习是人工智能（交叉学科，定位尚不清晰）的一个子领域；统计推断是统计学（一级学科）的一个分支（另一个分支是描述性统计学）
机器学习更关注最小化预测误差的某种度量，比如模型的泛化能力、预测的准确率或召回率；统计推断认为更关注推断本身，比如模型或参数的显著性水平、置信度以及统计量意义

二、频率学派和贝叶斯学派

统计推断是通过样本推断总体的统计方法，它是统计学的一个庞大的分支。统计学有两大学派，频率学派和贝叶斯学派，在统计推断的方法上各有不同。我们可以从频率学派和贝叶斯学派的长期争论历程中去了解两个学派的方法和观点，以及统计推断的相关知识:

频率学派，20世纪初期建立，在之后的整个20世纪基本主宰了统计学，代表人费舍尔（Fisher）、K.皮尔逊（Karl Pearson）、内曼（Neyman），费舍尔提出极大似然估计方法（Maximum Likelihood Estimation，MLE）和多种抽样分布，K皮尔逊提出Pearson卡方检验、Pearson相关系数，内曼提出了置信区间的概念，和K.卡尔逊的儿子E.S.皮尔逊一起提出了假设检验的内曼-皮尔森引理；
贝叶斯学派（Bayesians），20世纪30年代建立，快速发展于20世纪50年代（计算机诞生后），它的理论基础由17世纪的贝叶斯（Bayes）提出了，他提出了贝叶斯公式，也称贝叶斯定理，贝叶斯法则。贝叶斯方法经过高斯（Gauss）和LapLace（拉普拉斯）的发展，在19世纪主宰了统计学。
抽象地说，两种学派的主要差别在于探讨「不确定性」这件事的立足点不一样，频率学派试图对「事件」本身建模，认为「事件本身就具有客观的不确定性」；贝叶斯学派不去试图解释「事件本身的随机性」，而是从观察事件的「观察者」角度出发，认为不确定性来源于「观察者」的「知识不完备」，在这种情况下，通过已经观察到的「证据」来描述最有可能的「猜的过程」，因此，在贝叶斯框架下，同一件事情对于知情者而言就是「确定事件」，对于不知情者而言就是「随机事件」，随机性并不源于事件本身是否发生，而只是描述观察者对该事件的知识状态。
具体来说，两种学派的主要差别是在对参数空间的认知上，即参数的可能取值范围。频率学派认为存在唯一的真实常数参数，观察数据都是在这个参数下产生的，由于不知道参数到底是哪个值，所以就引入了最大似然（Maximum Likelihood）和置信区间（confidence interval）来找出参数空间中最可能的参数值；贝叶斯学派认为参数本身存在一个概率分布，并没有唯一真实参数，参数空间里的每个值都可能是真实模型使用的参数，区别只是概率不同，所以就引入了先验分布（prior distribution）和后验分布（posterior distribution）来找出参数空间每个参数值的概率。
贝叶斯学派的贝叶斯方法由于其理论更符合我们解决问题的思路,推断过程中加入了过往经验,且由于计算机的发展有效地解决了贝叶斯方法的难推导和难计算等缺陷,在机器学习的各种应用上都大放光彩,但也由于其对先验知识的要求,导致不适合被使用在一些不适合加入先验知识\十分追求严谨的应用场景,比如制药\法律等;频率学派通过假设检验的统计方法可以有效解决制药\法律的推断问题,但实际上也有天然的缺陷(这一块扩展内容较多,以后有机会再讨论).

总的来说，两个学派现状是仍在互相争论，也在发展中互相借鉴。

三、最大似然估计和最大后验估计

两个学派对应了如下两种经典的推断方法：

频率学派（Frequentist）- 最大似然估计（MLE, Maximum Likelihood Estimation）
贝叶斯学派（Bayesians）- 最大后验估计（MAP, Maximum A Posteriori）

用一个例子去更好地理解两种学派的对应两种方法，首先是一些名词的解释:

θ: 模型参数
x: 观察样本点
似然函数: 在字典中，似然（likelihood）和概率（probability）是差不多的意思，但在统计学里，似然函数和概率函数的含义却不同，对于形式为 $P(x|\theta)$ 的函数，如果θ是已知的，x是变量，这个函数叫做概率函数（probability function），描述的是不同的样本x出现的概率是多少; 如果x是已知的，θ是变量，这个函数叫做似然函数（likelihood function），描述的是不同的模型参数下，出现x这个样本的概率是多少。多个样本的离散型x的似然函数可表示为 $L(\theta) = \sum_{i=1}^{n}P(x|\theta)$ 。举个抛硬币的简单问题，如果有一枚硬币，连续抛两次，两次都正面朝上，那么该硬币的一次抛的结果正面朝上的概率是多少，换句话说就是硬币本身的不均匀程度是多少（大致可以想象成反面侧重量：总重量的比例）？对这个问题，我们先假设硬币均匀，硬币出现正面朝上概率p=0.5，那么出现两次正面朝上的概率是0.25，这个0.25是似然函数值，如果之前我们假设的是硬币不均匀，朝上概率p=0.6，那么出现两次正面朝上概率就成了0.36，似然函数值越大能表征θ成立的概率越大，但一定要注意似然函数值并不等于出现样本x时θ成立的概率，即更关注值的大小关系，而非值本身。
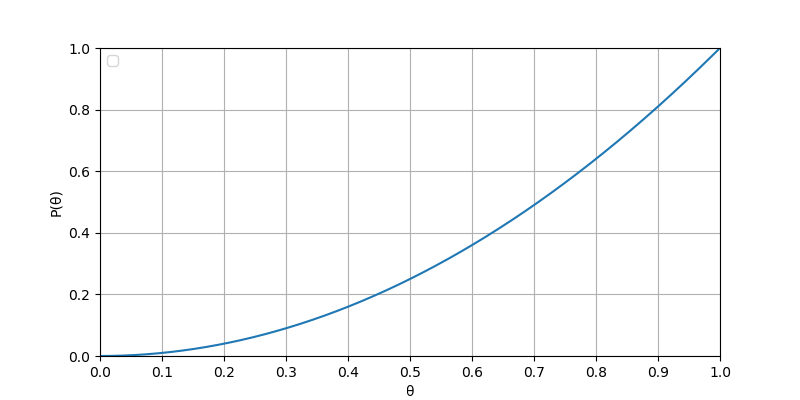
最大似然估计（MLE）: 频率学派的同学就是通过MLE方法解该问题，事实上前面抛两次硬币的例子中就进行了似然估计，其曲线可如图1表示，当p=0.5时，似然估计值为0.25；p=0.6时，似然估计值为0.36；在p=1.0时能取到最大似然估计值1.0。所以频率学派的同学们给出的答案是正面朝上概率是100%，硬币完全不均匀 ，虽然这个结论乍看之下很不合理，但其实想象一下，如果我们身处一个硬币就是完全不均匀的世界，我们并不会觉得这个结论不合理，所以我们在认为这个结论不合理的时候或许已经代入了日常生活的先验知识，这就引出了下面贝叶斯学派MAP方法的解题思路。

图1 抛两次硬币两次正面朝上的似然函数

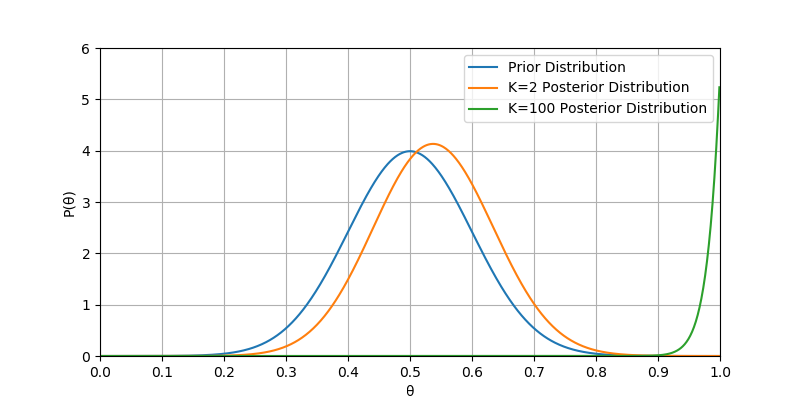
最大后验估计（MAP）: 贝叶斯学派的同学的解题思路与频率学派的同学不同，他会将先验知识加入到解题参考中，用最大后验估计的方法解题。他通过贝叶斯公式 $P(\theta|x_0)=\frac{P(x_0|\theta)P(\theta)}{P(x_0)}$ 来得到硬币朝上概率的概率分布。同样是两抛次硬币的例子，MLE方法通过抛两次硬币的样本得出是硬币朝上概率最可能是1.0的结论，他会觉得这个结论不可信，因为就他以前对硬币的认知，通常情况下硬币是接近均匀的，朝上的概率一般是0.5，最大后验估计就是在推断的过程中，通过贝叶斯定理将上述的这个先验知识考虑进去。对于投硬币的例子来看，他认为（先验地知道）θ取0.5的概率很大，取其它值相对较小，用一个高斯分布来具体描述我们掌握关于θ的这个先验知识，比如假设 $\theta $\sim$ N(0.5,0.1^2)$ ，即θ服从均值0.5，方差0.1的正态分布，函数如图2中”K=2 Prior Distribution”曲线所示，则最后后验估计函数为 $P(\theta|x)=\frac{\theta^2e^{-\frac{(\theta-\mu)^2}{2\sigma^2}}}{F\sqrt{2\pi}\sigma},\mu=0.5,\sigma=0.1$ ，其中F为函数从0到1的定积分，函数如图2中Posterior Distribution曲线所示，可以看到实验中硬币连续两次正面朝上只是将概率从0.5往右稍微拉偏了一点 。另外,当抛硬币的次数达到了100次,后验估计函数如图2中”K=100 Prior Distribution”所示（为了视觉友好，函数曲线在Y轴上压缩到了原值的0.1倍），可以看到θ的值越来越靠近1；事实上如果抛无穷大次硬币，都是正面朝上，那么无论先验假设是什么，后验分布都是1分布，即只在θ=1上概率不等于0。也就是说当抛无穷多次硬币都是正面朝上，贝叶斯派的同学才会跟频率学派的同学答题结果一样，都是硬币朝上概率就是1.0。

图2 抛硬币的先验分布和抛K次硬币K次正面朝上的后验分布

其实回头再对比一下MAP与MLE，当我们在MAP方法中，先验假设是 $\theta$\sim$U(0,1)$ ，即θ服从均匀分布时，MAP的目标函数和MLE目标函数就是同样形式的了，得出的结论会完全一致（当然这并非说明最大似然估计是最大后验估计的特例，前者的出发点就不一样）。从这可以看到，贝叶斯学派的同学解题很依赖一个良好的先验假设，否则MAP意义就不存在了。

参考文献

一、机器学习和统计推断的关系

二、频率学派和贝叶斯学派

三、最大似然估计和最大后验估计

FEATURED TAGS