上一篇文章介绍了机器学习的三要素-模型、策略、算法,但只是比较粗略地介绍,本文将着重介绍三要素之模型,视角主要放在不同模型间的区别上
本文首发于我的知乎专栏《机器怎么学习》中 机器学习·总览篇(5) 三要素之模型,转载请保留链接 ;)
机器学习首要考虑的问题是学习什么样的模型,如在《机器学习·总览篇(4) 机器学习的三要素》中描述的,模型就是所要学习的条件概率分布或决策函数。模型的假设空间(hypothesis space)包含所有可能的条件概率分布和决策函数,一般是无穷多种可能性,而训练(数据经过模型、策略、算法的处理,对模型的参数进行调整)的目的就是获取一个最优参数的模型。

一、非概率模型、概率判别模型、生成模型
模型通常有两种分类方式:第一种是按模型形式分类:概率模型(Probabilistic Model)和 非概率模型(Non-probabilistic Model);第二种是按是否对观测变量的分布建模分类:判别模型(Discriminative Model)和 生成模型(Generative Model)。这两种分类方法事实上把所有模型划分成了三类,可用图1清楚地表示,

具体说一下图1,从左到右分别是非概率模型(Non-probabilistic Model)、概率判别模型(Probalilistic Discriminative Model)、生成模型(Generative Model)。非概率模型和概率判别模型同属于判别模型(Discriminative Model),概率判别模型和生成模型同属于概率模型(Probalilistic Model)。分析三种模型,
I. 非概率模型(Non-probabilistic Model),直接对输入空间到输出空间的映射y=h(x)建模。实例:感知机(单层神经网络,Perceptron)、多层感知机(MLP)、支持向量机(SVM)、K近邻(KNN)
II. 概率判别模型(Probalilistic Discriminative Model):直接对后验概率P(y|x)建模,然后实现分类。实例:逻辑回归(LR)、最大熵模型(ME)、条件随机场(CRF)
III. 生成模型(Generative Model):对联合概率P(x,y)建模。如果是在聚类任务中,到这一步就结束了;但如果在分类任务中,再根据贝叶斯公式算出条件概率P(y|x),最后实现分类。实例:高斯判别分析(GDA)、朴素贝叶斯(NB)、受限玻尔兹曼机(RBM)、隐马尔科夫模型(HMM)
1.1 非概率模型(I)和概率判别模型(II)
两者共同点是都是判别模型,如图2表示,

图2是判别模型的分类示意图,非概率模型和概率判别模型的共同点是对判别标准直接建模,都是与图中的线一样判别(划分)数据。
非概率模型和概率判别模型的差别是判别数据地标准不一样,具体如下,
- 非概率模型的判别标准是一个超平面,超平面分割数据起到判别作用;
- 概率判别模型的判别标准是一个由条件概率表示的判别函数,根据条件概率的值大小比较起到判别作用。
1.2 生成模型(III)
生成模型与上述两种模型(判别模型)的差别是生成模型在类内对联合概率分布的建模,以此为基础再做分类,如图3所示,
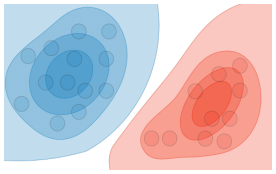
相比与图3中所示的生成模型对联合概率分布建模,而非概率模型和概率判别模型都没有对类内联合概率分布建模这一步。
1.3 小结
Stackoverflow上,有一个的简单例子能很好地说明以上三种模型的特点。假设特征x是1维,并且值只有1和2可选;标签y的也是1维,且值只有0和1可选,现在有如下 (x,y) 形式的4个样本 - (1,0)、(1,0)、(1,1)、(2, 1),则学习到的联合概率分布如下:
| y = 0 | y = 1 | |
|---|---|---|
| x = 1 | 1/2 | 1/4 |
| x = 2 | 0 | 1/4 |
这个联合概率分布就是生成模型的直接建模目标。而学习到的条件概率分布如下:
| y = 0 | y = 1 | |
|---|---|---|
| x = 1 | 2/3 | 1/3 |
| x = 2 | 0 | 1 |
这个条件概率分布就是概率判别模型的直接建模目标。而学习到的直接映射如下:
| y = 0 | y = 1 | |
|---|---|---|
| x = 1 | 1 | 0 |
| x = 2 | 0 | 1 |
这个分类标准就是非概率模型的建模目标。可以很清楚地看到三种模型信息量从多到少:生成模型 > 概率判别模型 > 非概率模型。更全面的总结可用表示为,
| 直接目标 | 数据量 | 模型信息 | 分类准确率 | 示例 | |
|---|---|---|---|---|---|
| 非概率模型 | 分类 | 少 | 少 | 相对较高 | SVM/NN/KNN |
| 概率判别模型 | 后验概率 | 中 | 中 | 相对较高 | LR/ME/CRF |
| 生成模型 | 联合概率 | 多 | 多 | 相对较低 | GDA/NB/HMM |
二、线性模型和非线性模型
x是模型函数的自变量,y是模型函数的因变量,上文中对于生成模型和判别模型本质差别是对于y是间接求解还是直接求解,对于概率模型和非概率模型的本质差别是y的表示形式,而在本小节中,我们还可以根据y与x的关系来区分线性模型和非线性模型。
2.1 线性模型
典型的线性模型有线性SVM和感知机(单层NN),两者都可以用y=wx+b的形式表示,y与x的关系是线性的;进行分类任务时,数据的判别分割界面都是线性平面。
对于逻辑回归模型,y=sigmoid(wx+b),y与x的关系是非线性的;然而,进行分类任务时,数据的分割界面仍然是线性平面。逻辑回归模型实际上我们称之为广义线性模型(Generalized Linear Model,GLM),GLM是线性模型的扩展,逻辑回归模型是y服从伯努利分布下的GLM;线性模型也可以看成是一种特殊的GLM,可以看成是y服从高斯分布下的GLM。GLM通过采用对应的联系函数针对不同y分布的数据,让y的取值范围与预测值范围一致,以及让模型比较好地拟合当下的数据。
其实,在统计意义上,如果一个回归方程是线性的,那么它的相对于参数就必须也是线性的;如果方程相对于参数是线性,那么即使性对于样本变量的特征是二次方或者多次方,这个回归模型也是线性的。所以广义线性模型本质上还是线性模型。后面会在有监督学习篇中详细介绍广义线性模型。
2.2 非线性模型
以上常见的线性模型通过特定的非线性变换,可以成为处理非线性可分数据的非线性模型,
| 通常采用的非线性变换方法 | |
|---|---|
| SVM | 非线性核函数 |
| LR | 非线性核函数 |
| NN | 多层堆叠 |
还有一些常见的天然非线性模型,如KNN、决策树(DT)、随机森林(RF)、GBDT等。另外,朴素贝叶斯模型用于分类时,假设对于每一维x和每一类y,x|y 条件概率满足高斯分布:任意维x在不同类别y下,如果 x|y 分布的方差都相等,则是线性分类器;如果 x|y 的方差不同,则是非线性分类器,具体分析可参考《朴素贝叶斯分类器本质上是线性分类器》一文。
参考文献
- 《统计学习方法》 李航
- Stanford CS 229 ― Machine Learning
- zhihu: 机器学习系列-广义线性模型
- 机器学习中线性模型和非线性的区别
- csdn: 机器学习之核函数逻辑回归(机器学习技法)
- souhu: 说人话的统计学
- jianshu: 机器学习面试之最大熵模型
- jianshu: 朴素贝叶斯分类器本质上是线性分类器