上一篇文章介绍了机器学习三要素中的第一个要素-模型,模型部分限制了预测模型函数的假设空间。本文将要介绍的第二个要素-策略,策略部分就是要定量判断不同参数下模型的优劣,为第三步求解最优模型做基础。由于策略部分想要介绍的内容较多,所以分成了两篇,这是第一篇,主要是对正则化系数和损失函数的介绍。
本文首发于我的知乎专栏《机器怎么学习》中机器学习·总览篇(6) 三要素之策略 - 损失函数,转载请保留链接 ;)
机器学习的学习目标是获得假设空间(模型)的一个最优解,在模型部分,我们固定了模型函数的形式,在此基础上选择最优参数即可。那么对于任意参数的模型,如何评判解是参数是优还是不优?如下图1中所示的一个线性回归和线性分类的例子,
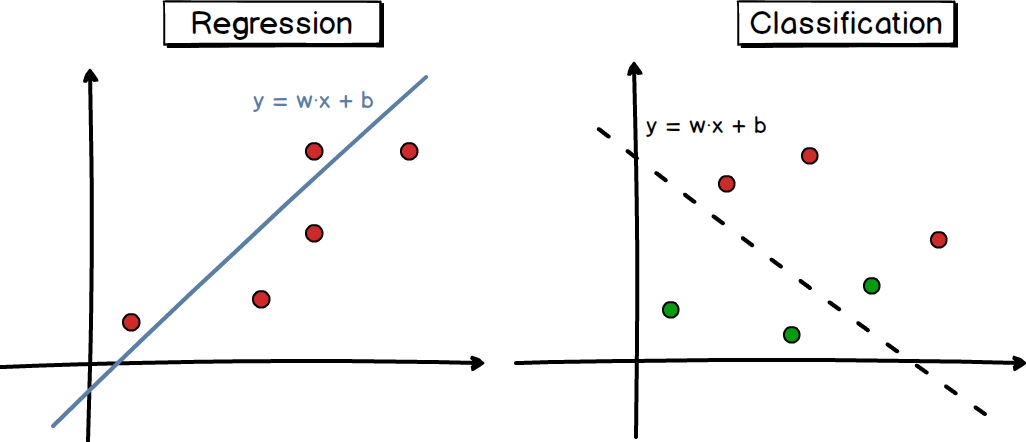
如图1所示,图中左子图是一个回归(Regression)任务,随意画一条拟合线性函数曲线,拟合效果看起来还不错,但定量的来看,到底有多不错?又比如右子图所示是一个分类(Classification)任务,随意画一条判别线性函数曲线,分割效果看起来也还行,但定量的来看,到底有多还行?这就引出了文本要介绍的内容-机器学习三要素的第二个要素-策略。策略部分就是评判“最优模型”(最优参数的模型)的准则和方法。图2所示就是策略的函数形式,
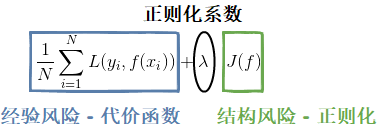
如图2所示的函数即经验结构风险的度量函数,也被称为目标函数(Object function),我们的优化目标就是选取最优的模型参数使目标函数的函数值最小,符合这个优化目标的模型就是最优的。目标函数由两部分组成,经验风险和结构风险:经验风险越小意味着模型在训练样本集上预测越准确,经验风险由代价函数表征,通过使模型预测值与训练样本标签尽可能接近来实现;结构风险越小意味着模型越简单,结构风险由正则化项表征,通过使模型参数尽可能小来实现。将经验风险和结构风险放在一起就要考虑权衡问题了,只有权衡两者才能尽可能地减少学习误差。所以我们要解决的第一个问题就是处理经验风险和结构风险的平衡问题(本文的第一节);然后再分析代价函数(本文的第二节)和正则化项(下一篇文章)各自应该如何选择。
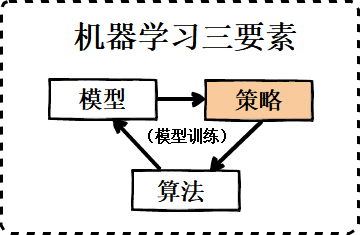
一、经验风险和结构风险的平衡
直接从机器学习模型的预测误差来分析,机器学习中的Error(误差)来源主要为Bias(偏差)、Variance(方差)以及Irreducible error(Noise,噪声),由如下公式表示,
其中,Bias是模型真实预测结果的期望与理论误差下界模型预测结果的偏差,可以简单理解成误差的期望;Variance是指相同大小、不同训练集训练出来的模型的预测结果与模型预测期望的方差,可以简单理解成误差的方差;Irreducible error是理论误差下界模型的泛化误差,它刻画了问题本身的难度,可以理解成无法避免系统误差。关于Bias和Variance更形象的表示如图3所示,
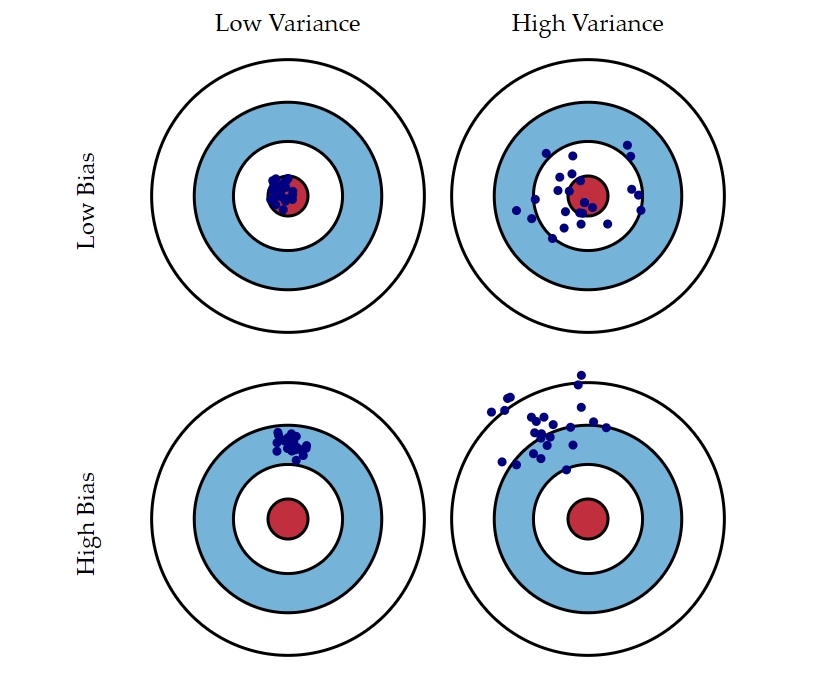
图3中一个蓝色的点表示一个模型的预测效果:低Bias能让模型的预测期望靠近靶心,低Variance能让模型预测表现得更稳定。在统计与机器学习领域权衡 Bias 与 Variance 是一项重要的任务,因为它可以使得用有限训练数据训练得到的模型更好地范化到更多的数据集上,如图4所示,
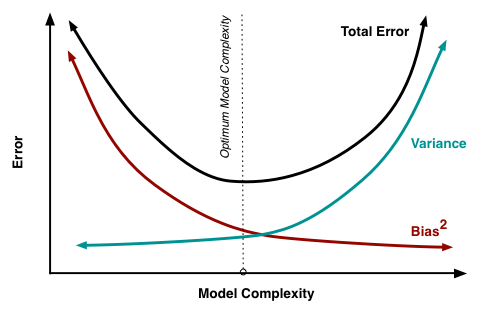
从图4中可以看到,Bias和Viriance虽然不能两全,但通过好的权衡,达到总体来说好的效果,如图3中的Total Error黑色曲线的最低点。经验风险会直接影响Bias,结构风险会直接影响Variance,所以对于目标函数来说,代价函数和正则化项本身不在同一个度量衡上,所以通常会在正则化函数前面加一个大于0的正则化系数 λ :λ 过小意味着正则化约束弱,对模型的复杂度惩罚过小,模型高Virance,对训练数据过拟合;λ 过小意味着代价函数约束弱,对模型的复杂度惩罚过大,模型高Bias,对训练数据欠拟合。选取合适的 λ 是一门“艺术”,跟下一篇文章选取学习率(learning rate)的值类似,可以有很多种方法。当然也有办法自动选择正则化参数 λ,具体选取方法可参考[4]和[5]两篇文章。
对目标函数的含义有了大概的了解,接下来重点是代价函数和正则化项:
- 代价函数是样本集的损失函数之和,本文的第二节直接主要介绍损失函数;
- 正则化是对wx+b中参数w的约束,下一篇文章将介绍正则化。
二、损失函数
损失函数,即Loss Function,如上文所说,是对经验误差的惩罚。下面我们将比较全面地介绍各种损失函数,为了方便理解,可以将分类问题和回归问题的损失函数分开考虑。
2.1 分类模型的损失函数
分类模型的损失函数按函数形式分有以下常见类别:
| 应用模型 | 函数形式 | |
|---|---|---|
| 0-1 loss | PLA [6] | |
| Hinge loss | SVM | |
| log loss | LR | |
| exponential loss | Boosting | |
| perceptron loss | Perceptron |
其中对于函数形式这一列,在分类任务中,m=y·f(x)。0-1 loss也称Goal Standard,非凸函数,一般不会直接用,通常在实际的使用中只将0-1损失函数作为一个预测的衡量标准,而更多地选择它的代理函数作为损失函数,不同的机器学习模型对应的损失函数通常比较固定,有一一对应的关系,比如:SVM用的是Hinge loss,LR用的是log loss,Adaboost用的是exp loss,感知器用的是perceptron loss。以上5种损失函数的”y*f(x)-L”的函数关系曲线如下图5所示,
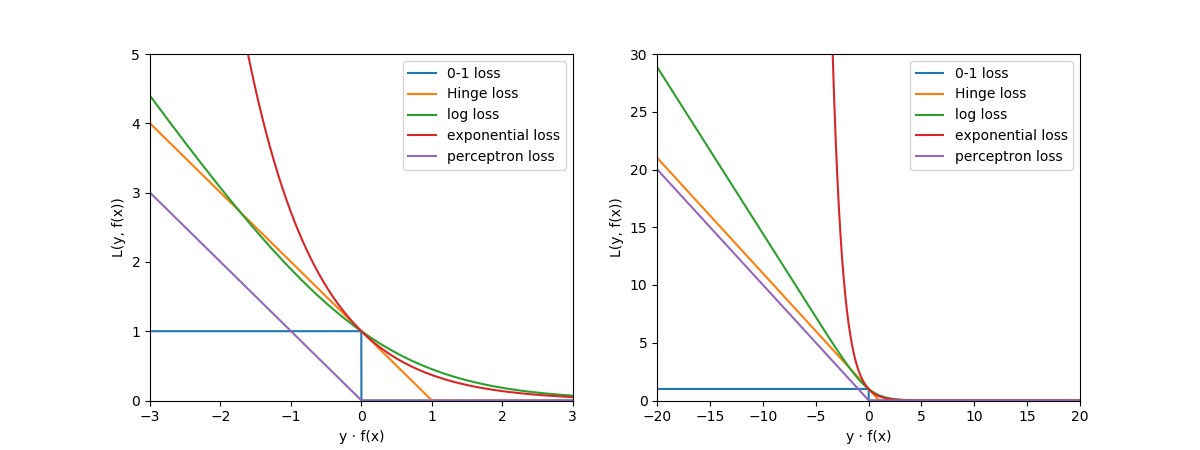
从图5可以看到,对于分类模型的损失函数:
- 如左子图所示,无论是哪种损失函数,本质上都是希望成为0-1 loss的代理,尽可能地继承0-1 loss的完美判别属性的同时,又能有凸函数的性质。可以看到无论是Hinge loss,log loss,exponential loss还是perceptron loss,它们在横轴0点的某一侧(事实上整体都是)都是凸函数,凸函数对于函数求解可是重大利好,所以这一点十分重要。
- 如右子图所示,有一个一飞冲天的loss,即的exponential loss,由于它在离0点较远处惩罚值相当大,所以对训练样本的离群点反应强烈,鲁棒性不好,这个问题也成了使用exponential los的boosting算法的天然缺陷。
2.2 回归模型的损失函数
回归模型的损失函数按函数形式分有以下常见类别:
| 应用模型 | 函数形式 | |
|---|---|---|
| squared loss | OLS | |
| absolute loss | ||
| log-cosh loss | XGBoost | |
| Huber loss | ||
| ϵ−insensitive loss | SVR | |
| Quantile loss |
其中对于函数形式这一列,在回归任务中,a=y-f(x);另外,abs(a)表示a的绝对值(由于latex的绝对值符号与markdown格式的表格冲突了,只能用abs来表示一下)。OLS(最小二乘法)用的是squre loss,XGBoost一般用的是log-cosh loss,SVR用的是ϵ−insensitive loss,对于神经网络回归或者直接回归,很多不同的损失函数互相替换都可以work,只有表现效果上的差别。以上6种损失函数的”(y-f(x)) - L”的函数关系曲线如下图6所示,
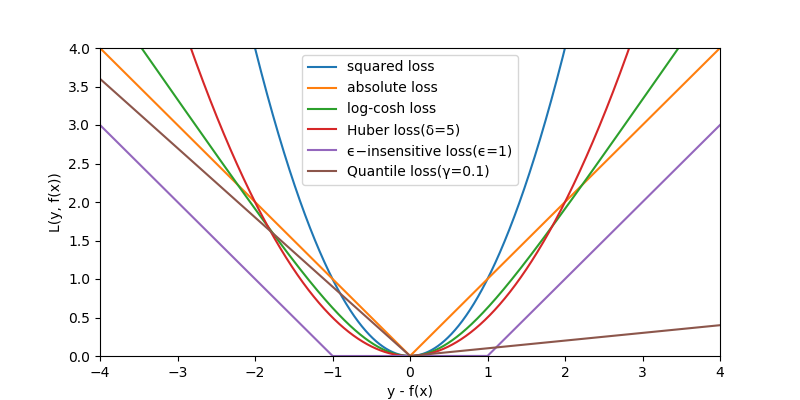
可以从图6中看到,对于回归模型的损失函数:
- 损失函数通常是以0处轴对称的,这个很容易理解,因为对于回归问题通常是假设向上偏差m和向下偏差都是同等偏差m,Quantile loss除外,因为它假设向上偏差和向下偏差不是同等偏差;
- SVR用的ϵ−insensitive loss有点特殊,它不经过原点,因为它假设允许有一定的偏差范围都不算偏差(回归曲线的上下偏差m形成的宽度为2m的管道状范围内惩罚都为0)
- loss可以按在0处是否可导分成两大类,不可导的性质在求函数最优解的时候处理麻烦,所以在实际应用中通常是采用0点处可导的loss;
- 这里又要点名批评一下一飞冲天的loss,对于回归任务来说,这个loss是squared loss,也是我们常说的MSE(mean squared error),虽然它在0处可导,但存在与分类任务中的exponential loss类似的问题:由于它在离0点较远处惩罚值相当大,对离群点鲁棒性不好。
小结:一个好的损失函数是具有凸函数性质、最好是处处可导、对离群点惩罚不要过大。损失为什么就有限的几种?因为自己搞些复杂的损失函数并不能保证是凸优化问题。损失函数还是可以有多种选择的,总有一款适合你。
由于如果在这一篇文章中还介绍正则化的话,内容有点太多了,所以决定放在下一篇文章详细介绍。
- blog: Understanding the Bias-Variance Tradeoff
- cnblogs: 理解 Bias 与 Variance 之间的权衡
- cnblogs: 机器学习之正则化
- DTU: Choosing the Regularization Parameter
- Paper: Methods for Choosing the Regularization Parameter
- blog: Perceptron Learning Algorithm
- csdn: 机器学习中的常见问题——损失函数