机器学习 · 总览篇 VIII - 蔡康的博客

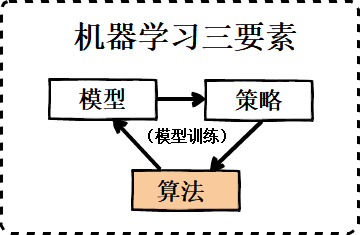
机器学习最后一个要素-算法，准确来说是优化算法，特别是数值优化（Numerical Optimization）或凸优化（Convex Optimization），属于运筹学（最优化理论）的一部分。机器学习中广泛使用的凸优化方法主要分为梯度下降法和拟牛顿法，这两类方法都派生出大量的变种，本文将介绍梯度下降法及其变种。

文章首发于我的博客，转载请保留链接 ;)

一、运筹学和凸优化

本文要介绍的机器学习最后一个要素-算法，其实就是使用了运筹学、特别是凸优化的相关知识，所以本文首先分别介绍运筹学和凸优化。

1.1 运筹学

运筹学（最优化理论）的研究范畴就是解决最优化问题。运筹学在机器学习领域应用非常广泛，因为机器的学习过程简单来说，做的主要就是优化问题：先初始化一下权重参数，然后利用优化方法来优化这个权重，直到目标函数不再下降、准确率不再上升，迭代停止。那到底什么是最优化问题？它的一般形式是：

$\begin{aligned} min f(x) \\ s.t.\text{ }x\in X \end{aligned}$

根据这个定义，上篇文章介绍的机器学习第二要素策略的目标函数，

$min\text{ }\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i)) \\ s.t.\text{ }g(f)\leq0,\text{ }g(f)=J(f)-\alpha$

就属于最优化问题。根据 f(x) 和 X 形式的不同将最优化问题分为以下问题：

线性规划。当目标函数 f 是线性函数而且变量约束 X 是由线性等式函数或不等式函数来确定的，这类问题为线性规划。
整数规划。当 X 包含对变量的整数变量约束，这类问题为整数规划。
非线性规划。目标函数 f 或变量约束 X 中包含非线性函数，这类问题为非线性规划。
网络流优化。当 X 包含连同赋权有向图约束，这类问题为网络流优化，物流、电网、通讯网络甚至是滴滴拼车等调度规划应用都属于该范畴。
随机规划。当 X 要求部分或全部变量是随机变量，这类问题为随机规划。随机规划需要分析随机变量的概率分布，以及各随机变量的自相关和互相关，求解方法比确定性规划复杂得多。
其它：有目标优化、鲁棒优化、最优控制等等。

1.2 凸优化

运筹学中一类重要的优化问题是凸优化，凸优化 = 凸集（约束条件）+ 凸函数（目标函数）+ 目标函数存在一阶导为0。如果要判定一个问题属于凸优化问题，那么首先需要约束 X 满足凸集，凸集的几何意义表示为：如果集合 C 中任意2个元素连线上的点也在集合 C 中，则 C 为凸集，可以用图1表示，

图1 非凸集和凸集的示例

，然后是满足目标函数是凸函数的要求，凸函数是一个定义在某个向量空间的凸子集 C（区间）上的实值函数 f ，而且对于凸子集 C 中任意两个向量， f((x1+x2)/2)>=(f(x1)+f(x2))/2，则 f(x) 是定义在凸子集c中的凸函数，可以用图2表示，

图2 非凸函数和凸函数的示例

可以看到凸问题要求是比较严格的，属于一类特殊的最优化问题。解决凸优化问题的过程称之为凸优化，凸优化具有以下特性：

局部最优解 = 全局最优解，是目前技术比较确定可以求解的非线性规划方式，且效率高
许多非凸问题通过一定的手段，转换成凸问题求解。要么等价地化归为凸问题，要么用凸问题去近似、逼近。典型的如几何规划、整数规划，它们本身是非凸的，但是可以借助凸优化手段去解，这就极大地扩张了凸优化的应用范围
在非凸优化中，可以借助凸优化方法，
- 当你要解决一个非凸优化问题时，可以先试图建立一个简化多凸优化模型，解出来以后作为非凸问题的一个起始点。
- 很多非凸优化问题的启发式算法的基础都是基于凸优化
- 可以先建立非凸优化的松弛问题，使用凸优化算法求解，作为非凸优化问题的上限或下限

1.3 机器学习中的凸优化

机器学习中对目标函数的求解（即三要素之算法），主要使用的就是上文说的凸优化方法：

“线性规划” 与 “目标函数与约束函数都是凸函数的非线性规划”，都属于凸优化。这类问题在机器学习中十分常见：比如线性回归（Linear Regression） 是线性规划，属于凸优化；比如常见的支持向量机（SVM） 和逻辑回归（Logistic Regression） 都是目标函数与条件函数都是凸函数的非线性规划，也属于凸优化。
对于非凸优化，通过一定手段，可以等价化归为凸问题。比如对于 “变量要求是整数、目标函数与约束函数都是凸函数” 的整型规划，可以通过凸松弛手段转换成凸优化问题。另外，对于非凸的优化问题，我们可以将其转化为对偶问题，对偶函数一定是凹函数，但是这样求出来的解并不等价于原函数的解，只是原函数的一个确下界，关于这一点可以看前一篇介绍正则化时说到的拉格朗日乘子法，不论原问题是不是一个凸优化问题，只要满足KKT条件，转换成的对偶问题就是一个凸优化问题，可以用凸优化方法求解。
对于非凸优化，在机器学习中直接用凸优化的手段去求最优解效果也不错，这跟做Optimization时的结论完全相反，这个现象与机器学习中各种正则化和随机化方法有关，从这里可见机器学习的工程性。比如深度学习（Deep Learning） 的目标函数就是高度非凸目标函数，然而我们通常也是直接上凸优化方法。

机器学习中常用的凸优化算法分为两大类：梯度下降法（Gradient Descent）和拟牛顿法（Quasi-Newton Methods）。因为两类方法的变种很多，所以拆分成两篇文章分别进行介绍，本文第二节将介绍梯度下降法及其变种，下一篇文章介绍拟牛顿法及其变种，两大类的主要差别也将在下篇文章中介绍。

二、梯度下降法及其变种

2.1 梯度下降法（Gradient Descent, GD）

想象你在一个山峰上，在不考虑其他因素的情况下，你要如何行走才能最快的下到山脚？当然是选择最陡峭的地方，这也是梯度下降法的核心思想：它通过每次在当前梯度方向（最陡峭的方向）向前迈一步，来逐渐逼近函数的最小值。假设在第n次迭代中，

$\theta_n = \theta_{n-1}+\Delta \theta$

我们将目标函数在 θn-1 处进行一阶泰勒展开：

$L(\theta_n)=L(\theta_{n-1}+\Delta\theta)\approx L(\theta_{n-1})+L^{'}(\theta_{n-1})\Delta\theta$

为了使 L(θ) 迭代后趋于更小的值，可以假定以下所示第一行条件，

$\begin{aligned} \Delta\theta&=-\alpha L'(\theta_{n-1}), \alpha>0 \\ \text{ s.t. } L(\theta_n)&=L(\theta_{n-1})-\alpha L^{'}(\theta_{n-1})^2 \\ &\leq L(\theta_{n-1}) \end{aligned}$

故迭代方式可以用如下公式表示，

$\theta_n=\theta_{n-1}-\alpha L'(\theta_{n-1})$

，需要注意的是，梯度下降法一次迭代是针对一个维度方向进行下降。目标函数关于模型参数的一阶导 L′(θn) 在不同的方法中都会使用到，为了方便起见，后文用 gn 来代替 L′(θn) ，新的迭代方式如下所示，

$\theta_n=\theta_{n-1}-\alpha g_{n-1}$

梯度下降法根据每次求解损失函数 L 带入的样本数，可以分为：全量梯度下降（计算所有样本的损失），批量梯度下降（每次计算一个batch样本的损失）和随机梯度下降（每次随机选取一个样本计算损失）。现在所说的 SGD（Stochastic Gradient Descent，随机梯度下降）多指Mini-batch Gradient Descent（批量梯度下降）。

优点：求一阶导，操作简单，计算量小，在损失函数是凸函数的情况下能够保证收敛到一个较好的全局最优解。

缺点：α是个定值，收敛的好坏受它的直接影响，过小会导致收敛太慢，过大会导致震荡而无法收敛到最优解。对于非凸问题，只能收敛到局部最优，并且没有任何摆脱局部最优的能力，因为一旦梯度为0就不会再有任何变化。

2.2 GD迭代方向的改进

一类常见的变种是对迭代方向 g 进行改进，即调整 GD 的迭代公式的梯度部分，

$\theta_n=\theta_{n-1}-\alpha g_{n-1}$

最常用的是以下3种改进，

2.2.1 Momentum

SGD 具有收敛不稳定性：在 SGD 中，参数 θ 的迭代变化量都只是与当前梯度正相关，这会导致在迭代过程中，θ在最优解附近以较大幅度震荡无法收敛。Momentum 能在一定程度上缓解 SGD 收敛不稳定的问题，它的思想就是模拟物体运动的惯性：当我们跑步时转弯，我们最终的前进方向是由我们之前的方向和转弯的方向共同决定的。Momentum 在每次更新时，保留一部分上次的更新方向：

$\Delta\theta_n = \rho\Delta\theta_{n-1}+ g_{n-1}$

优点： 1. 由于在迭代时考虑了上一次 θ 的迭代变化量，所以在最优解附近通常具有梯度因方向相反而抵消的效果，从而在一定程度上缓解 SGD 的收敛不稳定问题；2. 除此之外，Momentum 还具有一定的摆脱局部最优的能力，如果上一次梯度较大，而当前梯度为0时，仍可能按照上次迭代的方向冲出局部最优点。对于第一点直观上的理解是，它可以让每次迭代的“掉头方向不是那么大”，具体如图3所示，

图3 SGD（左）与 Momentum SGD 的对比（右）

，图3左子图为 SGD ，右子图为 Momentum 。可以看到，Moumentum 一方面能抑制 SGD 在来回振荡维度的迭代幅度，又能加强在缓慢单调变化维度的迭代幅度，

缺点：这里又多了另外一个超参数 ρ 需要我们设置，它的选取同样会影响到结果 。

2.2.2 Nesterov Momentum

Nesterov Momentum 又叫做 Nesterov Accelerated Gradient（NAG），是基于 Momentum 的加速算法。Momentum（也称之为Plain Momentum）的 θ 迭代向量的计算是把上一次迭代向量作为本次预期迭代向量，在此基础上叠加上本次梯度。而 NAG 认为这样的迭代不合理，迭代速度也不够快，NAG认为：既然都把上一次迭代向量作为本次预期向量了，就应该预期到底，应该将当前梯度替换成预期梯度，即当前 θ 加上上一次迭代向量之后的新 θ 所在点的函数梯度，公式表示如下，

$\Delta\theta_n =\rho\Delta\theta_{n-1}+ g(\theta_{n-1}-\alpha \Delta\theta_{n-1})$

，为了更直观比较 Nesterov Momentum 和 Plain Momentum 的差别，将两者的迭代式子相减比较，再用微分的思想看待，如下所示，

$\begin{aligned} \Delta\theta_n^{NM}-\Delta\theta_n^{PM}&=g(\theta_{n-1}-\alpha\Delta\theta_{n-1})-g(\theta_{n-1}) \\ &=\alpha \theta_{n-1}g'(\theta_{n-1}) \end{aligned}$

由于 g 是一阶导（最开始的定义，g(n) = L’(n)），而 Plain Momentum 只用到一阶导，两者相减的式子涉及到了二阶导，所以看出 Nesterov Momentum 实际隐含使用到了二阶导数的信息。二阶导数大于 0 则一阶导单调递增，也即 Nesterov Momentum 比 Plain Momentum 迭代幅度更大，因此可以加快收敛，从这里可以看到这种做法的内在理论：如果这次的梯度比上次大，那么我们有理由认为梯度还会继续变大，所以当前迈的步子可以更大一些。

直观地比较上述GD、Momentum GD、NAG三种梯度方法的迭代过程，如下图4所示，

图4 GD、Momentum GD、NAG迭代示意图

，上图指的是在同一维度方向上的迭代对比示意图，其中，绿色实线箭头表示上一次在某方向的迭代向量，蓝色实线箭头表示本次在该方向的迭代向量，绿色虚线箭头即 Momentum，第二个图中蓝色虚线箭头表示本次梯度向量，第三个图中浅蓝色虚线箭头表示预期梯度向量。

2.2.3 共轭梯度法（Conjugate Gradient）

梯度下降法一次迭代是针对一个维度方向进行下降，故它每一步都是垂直于上一步。而共轭梯度法本质是把目标函数分成许多方向，然后不同方向分别求出极值再综合起来。共轭梯度法最重要的问题在于，它分的方向不是原来的各个维度，因为那样没法保证最小值是每个维度的最小值。那么应该如何保证这一条件呢，就要借助共轭向量，共轭向量的定义如下，

通过一个不是很复杂的证明过程（有兴趣可以参考《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》一文中的第8节），可以证明在各个共轭向量都是最小值的点就是总最小值点，而且可以通过下面的式子来计算共轭向量，

，其中 r 是原本维度，d(i) 是上一次迭代的共轭方向，d(i+1) 就是这一次需要迭代的共轭方向。共轭梯度法迭代过程如图5所示，

图5 共轭梯度法迭代过程示意图

图5中第1个子图为 SGD 迭代过程，第2个子图为将 SGD 迭代过程平移合并在一起的模样，第3个子图为共轭梯度法迭代过程，可以看到共轭梯度法的迭代方向与原始维度方向不同。

优点：在n维的优化问题中，共轭梯度法最多n次迭代就能找到最优解。共轭梯度法其实是介于梯度下降法与牛顿法之间的一个方法，是一个一阶方法，但克服了梯度下降法收敛慢的缺点，又避免了存储和计算牛顿法所需要的二阶导数信息。

缺点：需要求解共轭，高维向量计算量过大，故不适用于高维参数向量的情况。

2.3 GD学习率的改进

不同于2.2节算法是对迭代方向进行改进，本节算法主要研究沿着梯度方向走多远的问题，也即如何选择更合适的学习率 α 。

$\theta_n=\theta_{n-1}-\alpha g_{n-1}$

以图6所示 Tensorflow 的 tf.Keras.Opitimizers 提供的方法为参考，本节将介绍以下常用的对学习率进行改进的GD，

图6 Tensorflow 的 tf.Keras.Opitimizers 提供的优化方法

2.3.1 Adagrad 《Adaptive subgradient methods for online learning and stochastic optimization》 2011

即 adaptive gradient ，自适应梯度法。它通过记录每次迭代过程中的前进方向和距离，从而使得针对不同问题，有一套自适应调整学习率的方法

$\alpha=\frac{1}{\sqrt{\sum_{i=1}^{n-1}g_{i}+\epsilon}}\alpha_0$

优点：解决了 SGD 中学习率不能自适应调整的问题 缺点：学习率单调递减，在迭代后期可能导致学习率变得特别小而导致收敛及其缓慢。同样的，我们还需要手动设置初始 α。

2.3.2 AdaDelta 《ADADELTA: An Adaptive Learning Rate Method 》 2012

AdaDelta 是在 Adagrad 提出的后一年提出，它解决了 Adagrad 面临的两个问题，即迭代后期可能导致学习率变得特别小而导致收敛及其缓慢的问题，以及初始学习率需要人为设定的问题，它的迭代公式如下所示，

$RMS[g]_{n}=\sqrt{E[g^2]_n+\epsilon}$ $E[g^2]_n=\rho E[g^2]_{n-1}+(1-\rho)g_n^2$ $\alpha=\frac{RMS[\Delta\theta]_{n-1}}{RMS[g]_n}$

，这里 ρ 为小于1的正数，随着迭代次数的增加，同一个会因为累乘一个小于1的数而逐渐减小，即使用了一种自适应的方式，让距离当前越远的梯度的缩减学习率的比重越小。

除此之外，分子是为了单位的统一性，其实上述的算法中，左右的单位是不一致的，为了构造一致的单位，我们可以模拟牛顿法（一阶导/二阶导），使单位一致，而上述分子就是通过这种方式最终推导出的结果，具体可以参考原文。这样，也解决了 Adagrad 初始学习率需要人为设定的问题。

2.3.3 RMSprop 《Overview of Mini-batch Gradient Descent》 2012

RMSprop 是大佬 Hinton 提出来的，其实它其实就是 AdaDelta，这里的 RMS 就是AdaDelta中定义的 RMS。有意思的是, AdaDelta 的提出者 Zeiler 就是 Hinton 的弟子，他不知道自己的老师已经给这种方法命了名字。下面是 Hinton 的演说PPT里的定义，

AdaDelta 与 RMSprop 核心思想是一样的，不过在提出的时候还是有一点小差别，AdaDelta 去掉了全局学习率，而 RMSprop 还是使用了全局学习率作为基准，。

2.3.4 Adam 《Adam: A Method for Stochastic Optimization》 2014

Adam 是 Momentum 和 AdaDelta 的结合体，我们先看它的更新公式，

$E[g^2]_n=\rho E[g^2]_{n-1}+(1-\rho)g_n^2$ $E[g]_n=\phi E[g]_{n-1}+(1-\phi)g_n^2$ $\bar{E[g^2]_n}=\frac{E[g^2]_n}{1-\rho^n}$ $\bar{E[g]_n}=\frac{E[g]_n}{1-\phi^n}$ $\alpha=\frac{\bar{E[g]_n}}{\sqrt{\bar{E[g^2]_n}}+\epsilon}\alpha_0$

它利用误差函数的一阶矩估计和二阶矩估计来约束全局学习率。

优点：结合 Momentum 和 Adagrad，稳定性好，收敛速度很快。同时相比于 Adagrad ，不用存储全局所有的梯度，适合处理大规模数据。有一说是Adam是世界上最好的优化算法，无脑用它就对了。

缺点：收敛速度虽快，但实际运用时往往没有 SGD 的解更优 ，关于这一点，最后2.4节的小结会具体介绍。

2.3.5 Adamax 《Adam: A Method for Stochastic Optimization》 2014 Section.7

Adamax 与 Adam 唯一区别在于 Adamax 在做二阶矩估计的时候，简化了取值，

$E[g^2]_n=\max(\vert g_n\vert,\rho E[g^2]_{n-1})$ $\alpha=\frac{\bar{E[g]_n}}{E[g^2]_n+\epsilon} \alpha_0$

2.3.6 Nadam 《Incorporating Nesterov Momentum into Adam》 2016

如提出 Nadam 的文章标题所述，Nadam 就是将 Nesterov Momentum 应用到 Adam。

2.4 小结

上文提到的迭代方法是GD一族，它们是机器学习中求目标函数最优解中最常用的方法，还有一些其它方法，但也是在常用方法的基础上做的小调整或者方法组合。除此之外，关于GD在机器学习中的应用还有下面两个值得一提的点，

本文2.2节中对GD迭代方向的改进和2.3节中对GD学习率的改进并不冲突，意味着两者可以各种组合 ，比如将 Nesterov Momentum 应用到 Adam 的 Nadam 就是一个典型的例子，还比如 Tensorflow 对 RMSprop 的实现就应用了 Plain Momentum。
从实际应用上来看，AdaDelta 及其后续改进算法到训练后期，进入局部最小值之后会反复在局部最小值附近抖动，而手动调整学习率的 Momentum SGD 在这种情况下效果更好。这是因为手动调整学习率的 Momentum SGD 幅度通常比 AdaDelta 学习率调整幅度大，故更容易从局部最小值附近抖出来。这也是为什么很多 state of art 的论文采用是 SGD 方法。

参考文献

机器学习 · 总览篇 VIII

三要素之算法 - 梯度下降法及其变种

一、运筹学和凸优化

1.1 运筹学

1.2 凸优化

1.3 机器学习中的凸优化

二、梯度下降法及其变种

2.1 梯度下降法（Gradient Descent, GD）

2.2 GD迭代方向的改进

2.3 GD学习率的改进

2.4 小结

FEATURED TAGS