机器学习 · 总览篇 X - 蔡康的博客

VC 理论中 VC维和 VC界作为机器学习可学习性的最重要的理论基础，对于机器学习方法的研究和使用具有十分重要的指导意义。比如对于一个任务，我准备使用的机器学习方法是否合理、数据量至少需要多少，这些问题如何在进行实验之前就能被解答？答案就在本文中。

文章首发于我的博客，转载请保留链接 ;)

机器学习主要研究的是怎么去学习解决一个问题，这里面包含了一个隐含的前提条件：对于待学习的问题，学习方法必须是可行的。那么怎么去判定一个学习方法对于问题的可学习性呢？PCA Learning 就是关于机器学习可学习性的一个完善的解释理论。PAC learning，全称是 Probably approximately correct learning，中文直译叫概率近似正确学习，有点拗口，解释下这个名称：

首先，Approximately Correct（近似正确）就是指学出的模型的误差比较小（误差被限制住），因为实现零误差（Absolutely Correct）是非常困难并且通常没有必要的，所以这里考虑的是 Approximately Correct；
其次，由于随机性的存在，我们只能从概率上保证 Approximately Correct 的可能性是很大的（存在一个概率下界）。

以上这就是 PAC Learning 的名称由来。Leslie Valiant 于1984年提出 PAC Learning，也主要因为该理论获得2010年图灵奖，可见该理论对机器学习的重要性。 PAC Learning 可以看做是机器学习的数学分析框架，它将计算复杂度理论引入机器学习，描述了机器学习的有限假设空间的可学习性，无限空间的VC维相关的可学习性等问题。

下面将从可学习性、VC界、VC维几个角度对 PAC Learning 理论进行介绍。在什么情况下 learning 是可行的？以机器学习实际应用的角度来看，需要具备以下两个条件，

模型不能过于复杂，数据量需要足够大，即模型的复杂程度不能远高于数据量的支撑
合适的最优化方法，即让目标函数值接近0 的求参算法

这两个条件看起来是 “经验主义”，那有没有更加准确的数学程式化定义？

一、Hoeffding不等式

为了解答上面的问题，需要从 Hoeffding不等式说起，Hoeffding不等式是关于一组随机变量均值的概率不等式。如果 X1,X2,⋯,Xn 为一组独立同分布的参数为 p 的伯努利分布随机变量，n为随机变量的个数。定义这组随机变量的均值为：

$\bar{X}=\frac{X_1+X_2+...+X_n}{n}$

那么对于任意 δ>0, Hoeffding不等式可以表示为

$P(|\bar{X}-E(\bar{X})|\geq \delta)\ \leq \ 2e^{-2\delta^2n}$

Hoeffding不等式可以直接应用到一个抽球颜色的统计推断问题上：我们从罐子里抽球，希望估计罐子里红球和绿球的比例，

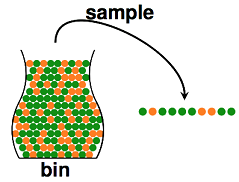
如果对总览篇III 一文中涉及的统计推断方法还记得的话，知道这个问题根据频率学派和贝叶斯学派的差别有两个不同的答案，频率学派给出的答案就是总体的期望 μ 就等于样本期望 ν，这里对两个学派就不再次进行解释了，只讨论频率学派给出的答案的准确性。直觉上，如果我们有更多的样本，即抽出更多的球，总体的期望 μ 确实越接近样本期望 ν；事实上，这里可以用 Hoeffding不等式量化地表示接近情况，如果抽球样本数维 N，则如下：

$P(|v-\mu|>\varepsilon )\ \leq \ 2e^{-2\varepsilon^2N}$

二、Hoeffding不等式应用到机器学习

将 Hoeffding不等式应用到机器学习的问题上，机器学习的过程可以程式化表示为：通过算法 A，在机器学习方法的假设空间 H 中，根据样本集 D，选择最好的假设作为 g，选择标准是使 g 近似与理想的方案 f，其中，H 可以是一个函数（此时是非概率模型），也可以是一个分布（此时是概率模型），g 和 f 属于 H。类似于上面 “抽球” 的例子，可以通过样本集的经验损失（expirical loss ） $E_{in}(h)$ ，即 in-sample error，来推测总体的期望损失（expected loss） $E_{out}(h)$ 。对于假设空间 H 中一个任意的备选函数 h，基于 Hoeffding不等式，我们得到下面的式子：

$P(|E_{in}(h)-E_{out}(h)|>\varepsilon)\leq\ 2e^{-2\varepsilon^2N}$

那么对于整个假设空间 H，假设存在 M 个 h，则可以推导出下面的式子：

$\begin{aligned}&P(|E_{in}(h)-E_{out}(h)|>\varepsilon)\\\leq\ &P(|E_{in}(h_1)-E_{out}(h_1)|>\varepsilon \ \cup \ ...\ \cup\ |E_{in}(h_M)-E_{out}(h_M)|>\varepsilon) \\ \leq \ & P(|E_{in}(h_1)-E_{out}(h_1)|>\varepsilon + \ ... + \ P(|E_{in}(h_M)-E_{out}(h_M)|>\varepsilon) \\ \leq \ & 2Me^{-2\varepsilon^2N} \end{aligned}$

上面这个式子的含义很重要：在假设空间 H 中，设定一个较小的 ϵ 值，任意一个假设 h ，它的样本值和期望值之间的误差概率被一个只与 ϵ、样本数 N、假设数 M 相关的值约束住。

到这里，我们可以将最开始看起来 “经验主义” 地对 learning 可行的情况定义用上面的结论改造一下，如下所示：

1. 如果备选函数集（假设空间 H）的大小 |H|=M ，M 有限，训练数据量 N 足够大，则对于学习算法 A 选择的任意备选函数 h，都有 $E_{in}(h)\approx E_{out}(h)$ 2. 如果 A 找到了一个备选函数，使得 $E_{in}(h)\approx 0$ ，则有很大概率使 $E_{out}(h)\approx 0$

所以将 learning 可行性的问题用上面两个结论转换一下，问题变成了：

1. 我们能否保证 E-in(h) 与 E-out(h) 足够接近？ 2. 我们能否使 E-in(h) 足够小？

其中对于第2点，能否使 E-in(h) 足够小这个问题通过合适的 “策略+算法” 可以达成，关于这一点在前面的文章中已经解释地比较详细了（具体可参考《总览篇 VI 策略-损失函数》、《总览篇 VIII 算法-梯度下降法及其变种》、《总览篇 IX 算法-牛顿法和拟牛顿法》这3篇文章）；对于1点，我们将在下文继续分析。

三、成长函数（Growth Function）

继续上文进行分析，对于假设函数 h，我们如果能够保证其在样本集中的损失值与其在总体数据集中的损失值之间高误差的概率存在一个接近 0 的上界，那么当然就能够保证 E-in(h) 与 E-out(h) 足够接近。从上文的最后结论着手继续分析，

$P(|E_{in}(h)-E_{out}(h)|>\varepsilon)\ \leq \ 2Me^{-2\varepsilon^2N}$

对于假设空间中的备选函数，假设数 M 通常是一个无穷大的数，而ϵ、样本数 N 是一个有限的数，看起来并不存在上界。所以一个直观的思路是，能否找到一个有限的因子来替代掉上面不等式上界（右边式子）中的 M。幸运的是，存在这个因子 m-H 恒满足下面的式子：

$P(|E_{in}(h)-E_{out}(h)|>\varepsilon)\ \leq \ 2\ D(m_H) \ e^{-2\varepsilon^2N}$

，且 m-H 是有限的，我们暂且称之为有效假设数（Effective Number of Hypotheses），D 是我们将 m-H 加入到上面的不等式替代大 M 的某种操作方法，我们先解决找到 m-H 的问题，再去解决 D 的问题。

为了找到 m-H 的值，继续进行分析：虽然假设空间中通常存在 M 个（M=无限）假设函数 h，但多个 h 之间并不是完全独立的，他们是有很大的同质性，也就是在 M 个假设中，可能有一些假设可以归为同一类。下面以二维线性假设空间为例，我们的算法要在二维空间挑选一条直线发成作为尽可能好的假设 g，用来划分一个点（N=1）的类别，虽然有无数条直线可供选择，但真正有判别意义的就两类：一类判别成正例，一类判别成反例。如下图所示，

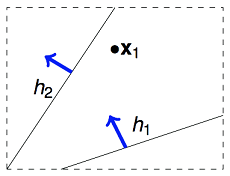
即对于二维线性假设空间，当 N=1 时， $m_H=2$ ，以此类推，可以用如下表格表示，

N=1	N=2	N=3	N=4
$m_H=2$	$m_H=4$	$m_H=8$	$m_H=14$

N 为1、2、3时，对应的有效假设数很好理解，但 N=4 时有效假设数是14而不是16，可以在纸上画一下 4 个点的两种不同的分布情况（凸轮廓和非凸轮廓）。根据以上的分析我们可以推测到一个结论，假设空间的大小 M 虽然是很大，但在样本集 D 上，有效假设数 m-H 是有限的，m-H 随着样本数 N 变化，有效假设数 m-H 和样本 N 关系又称之为成长函数（Growth Function），也就是样本损失值和总体期望损失值之间高误差的概率上确界（最小上界）。虽然上确界不能直观得出，但可以确定的是，

$m_H(N)\leq 2^N$

而且这个结论显然可以应用在任何二分类问题的假设空间，已知 m-H 必然存在一个上界是 2^N，则有下面的式子:

$P(|E_{in}(h)-E_{out}(h)|>\varepsilon)\ \leq \ 2^{N+1}e^{-2\varepsilon^2N}$

我们当然不会满足于成长函数是一个指数函数的结论，因为上式并不能保证概率上界（不等式的右边）是一个接近于0的值，所以我们需要进一步分析，尝试找到一个更小的上界。上面我们具体分析了二维线性假设空间下的情况，这里暂且不讨论二维假设空间中有效假设数的普遍结论，下文1.2节会详细讨论，下面我们来看更多其它情况下的案例。

第一种是 “正例射线” 的假设空间，如下图1所示，

图1 一维数据的 “正例射线” 的假设空间

根据排列组合知识，可知 “正例射线” 的假设空间下的成长函数是

$m_H(N)=\binom{N+1}{1}=N+1$

这个假设空间的有效假设数 m-H 是 N+1，是一个关于 N 的多项式，

$P(|E_{in}(h)-E_{out}(h)|>\varepsilon)\ \leq \ 2D(N+1)e^{-2\varepsilon^2N}$

OK，从上式的右边可以看到 N > 0 时，假设 D 是某种多项式操作方法，则上界（不等式右边）是一个随 N 递减的函数，当 N 取一个很大的值时，上界接近于0，对于这个问题，大功告成，是可学习的。

第二种是 “凸集” 的假设空间，如下图2所示，

图2 二维数据的凸集假设空间

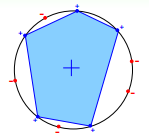
给定任意一种排列情况，总能找出一个凸集刚好包含了所有+1的点，并将-1的点排斥在外，所以很可惜，这种情况下的 m-H 就是 2^N，是不可学习的。

综合以上两种情况，我们发现，如果成长函数是指数函数，则随着 N 的增大，概率上界也急剧增加，所以我们希望成长函数是多项式，比如 “正例射线” 的问题，就是可学习的。那么是否有更多更普遍的成长函数是多项式的问题呢？幸运的是，答案又是肯定的。

四、打散（Shatter）、断点（Break Point）与边界函数（Bound Function）

继续上文分析，为了找到更普遍的成长函数是多项式的问题，需要了解两个概念：打散（Shatter）与断点（Break Point）。

打散很简单，上文的 “凸集” 问题中 m-H=2^N，我们就可以称之为：N 个样本全都能被 H 打散（Shatter）；而对于 “正例射线” 问题，当 N=1 时，m-H = 2 = 2^N，故称该问题中 1 个样本能被 H 打散。

断点与打散相关，不能被打散的样本数目就是断点，还是上面的 “正例射线” 问题，当 N>1 时，m-H 恒小于 2^N，故 N=2,3,4,… 都是断点。

总之，如果有 m-H(n) = 2^n，则称 n 个样本被 H 打散； m-H(n) < 2^n，则称 n 是 H 的一个断点，通常我们只关注最小断点值，称之为 k，因为大于 k 的点都是断点。接下来就是正餐，不同的假设空间 H 的断点 k 不一样大，我们定义一个上限函数 B(N,k)，称之为 Bound Function，边界函数，即成长函数 m-H 的上界，表示在断点为 k 时成长函数 m-H 的上界，理解断点可能有点困难，可以把它看成一个假设空间 H 的一个固有属性。根据上文，当然有 B(N,k) 不大于 2^N，具体有以下情况，

B(N,1)=1，因为 B(N,1) 表示对于 N 个样本，任意一个样本都不允许完全2分类，那么只能只有一种情况，加入任何第二种情况，总会有一个样本出现了两个分类;
B(N,N)=2^N-1，因为对于 N 个样本，如果没有断点，B=2^N，而在 N 处刚好有断点，那么去掉某一种情况，就可以满足了;
B(3,2)是多少，可以看下图3所示，

图3 3 个样本断点为 2 的边界函数值 B(3,2) 的演算

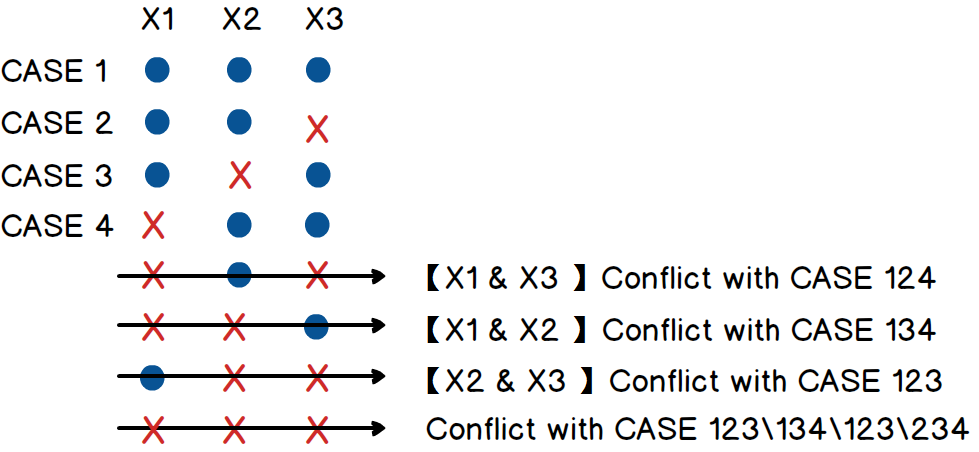
故，B(3,2)=4。以此类推，可以求得所有 B(N,k），但每个都这么算好麻烦，用计算机算比较快，但难道没有一个通用的表达式吗？看了一眼文章的进度条，看来答案是有的。

继续上文分析，根据1有 B(2,1)=1，根据2有 B(2,2)=3，根据3有B(3,2)=4。 B(3,2) 刚好等于 B(2,1)+B(2,2)，即刚好满足 B(N,k) = B(N-1,k) + B(N-1,k-1)，这不是偶然，我们可以大概推导一下（可以跳过，直接看结论）： B(N,k) 比 B(N-1,k) 多了一个新样本，但断点没变，假设 B(N,k) 中有一部分（2α 个）是由 B(N-1,k) 的一部分（α 个）复制了一遍，然后分别加上新样本两类的情况；另一种是不能复制，只能加上新样本特定某一类别的那部分（β 个）。由于 B(N,k) 中存在 2α 个复制出的 case 保证了断点是 k，这意味着把新样本去掉后，原始 α 个 case 需要保证 N-1 个样本时断点是 k-1，否则 2α 个 N 样本的 case 的断点必然不是 k。根据以上推导可以得到

$\begin{aligned} &B(N,k)=2\alpha+\beta\\ &B(N,k-1)=\alpha+\beta\\ &B(N-1,k-1)=\alpha\\ \Rightarrow B(N,k) & = B(N-1,k) + B(N-1,k-1) \end{aligned}$

，根据以上递推公式，可以通过数学归纳法求 B(N,k) 的表达式，熟悉的高考题味道 :) ，推导过程省略，结论就是，

$B(N,k)=\sum_{i=0}^{k-1}\binom{N}{i}$

当 N » k时，有如下近似：

$B(N,k)=\sum_{i=0}^{k-1}\binom{N}{i}\approx \binom{N}{k-1}\approx \lambda N^{k-1}$

这个式子表示，如果假设空间存在有限的断点（Break Point），那么成长函数 m_H(N) 会被最高幂次为 k–1 的多项式上界 B(N,k) 给约束住。

五、VC界

为了确保可学习性，是要保证对于假设空间 H 中的任意的 h，都要有 Bad Case（样本损失值和总体期望损失值之间高误差

$P(\exists h\in H\ s.t.\ |E_{in}(h)-E_{out}(h)|>\varepsilon)\ \leq \ 2\ D(m_H(N))\ e^{-2\varepsilon^2N}$

看起来将 N^(k+1) 替代上式的 m-H 就完成了，现在就来解决这个 D 问题，通过某种方法将 D 去掉，不能直接去掉 D 用 m-H 直接替代大 M 的主要问题在于：E-in 的可能取值是有限个的，但 E-out 的可能取值是无限的。怎么让不等式是针对有限的函数呢？可以通过将 E-out 替换为验证集 (verification set) 的 E-in’ 来解决这个问题。通过如下一系列复杂的证明，

$\begin{aligned} &(1)\ P(|E_{in}(h)-E_{out}(h)|>\frac{\varepsilon}{2})\leqslant P(|E_{in}(h)-E_{in}'(h)|>\frac{\varepsilon}{2})\\ &(2)\ P(|E_{in}(h)-E_{out}(h)|>\frac{\varepsilon}{2})+P(|E_{in}(h)-E_{in}'(h)|>\frac{\varepsilon}{2})=1 \\ &(3)\Rightarrow \ P(|E_{in}(h)-E_{out}(h)|>\frac{\varepsilon}{2}) \leq \frac{1}{2}\leq P(|E_{in}(h)-E_{in}'(h)|>\frac{\varepsilon}{2})\\ &(4)\Rightarrow P(|E_{in}(h)-E_{out}(h)|>\varepsilon) \leq 2P(|E_{in}(h)-E_{in}'(h)|>\frac{\varepsilon}{2}) \\ &(5)\Rightarrow P(|E_{in}(h)-E_{out}(h)|>\varepsilon) \leq 2m_H(2N)P^{fixed}(|E_{in}(h)-E_{in}'(h)|>\frac{\varepsilon}{2}) \\ &(6)\Rightarrow P(|E_{in}(h)-E_{out}(h)|>\varepsilon) \leq 2m_H(2N)P^{fixed}(|E_{in}(h)-\frac{E_{in}(h)+E_{in}'(h)}{2}|>\frac{\varepsilon}{4}) \\ &(7)\Rightarrow P(|E_{in}(h)-E_{out}(h)|>\varepsilon) \leq 2m_H(2N)e^{\frac{1}{8}\varepsilon^2N} \\ \end{aligned}$

终于将 D 给去掉，得到了我们要的 VC界表达式，即最后一行公式。其实推理过程不用太在意，最重要的是最后的不等式，结合 “m-H(N) 最高幂次为 k–1 的多项式上界 B(N,k) 给约束住” 的结论，有：

$P(|E_{in}(h)-E_{out}(h)|>\varepsilon) \leq 2^kN^{k-1}e^{\frac{1}{8}\varepsilon^2N}$

以上式子意味着，随着 N 的逐渐增大，指数式的下降会比多项式的增长更快，N 足够大时，对 H 中的任意一个假设 h，E-in(h) 都将接近于E-out(h)，这表示学习可行的第一个条件是有可能成立的。需要强调的是，以上所讲的只适用于二元分类问题，因为我们在推导断点、成长函数和边界函数时一直都基于二元分类这一前提。

六、VC维

上文的分析中可以看到，断点 k 是一个很重要的概念，而 VC维就是跟 k 强相关的一个概念，VC维（VC dimension）的定义是 H 最多能够打散的点的数量，故如果用 d-vc 来表示 VC维，那么明显有：

$d_{vc}=k-1$

联系上文，可以看到 VC界是基于 VC维的。上面对二维线性假设空间分析，已知二维线性分类器不能打散 4 个及以上的样本，即 k=4，所以对于二维线性分类器，它的 VC维就是3。一般而言，VC维越大，表达能力就越强，但对数据、学习策略和算法的要求也越高。对于一个给定的分类器或者假设空间，应该如何确定 VC维呢？一个不好的消息是，对于非线性分类器，VC维非常难于计算，在学术研究领域，这仍然是一个有待回答的开放性问题。一个好消息是，对于线性分类器 VC维是可以计算的，N 维实数空间中线性分类器和线性实函数的 VC维是 N+1。

七、深度学习与VC维

多层神经网络作为非线性分类器，VC维同样难以计算，但可以得到一个估计值。比如对于输出只有一维的深度神经网络，VC维如下所示：

$\begin{aligned} d_{vc}& =O(N\ log_2N) \\ N &= \sum_{i=1}^{l}\sum_{j=1}^{d_{i-1}}(d_{i-1}+1) \end{aligned}$

其中 l 是层数，d_i-1 是前一层的节点数，可以看到 VC维与网络层数和节点数个数相关。如果对具体证明过程感兴趣，可以参考论文《VC Dimension of Multilayer Neural Networks, Range Queries》

举例来说，一个普通的三层全连接神经网络：input layer 是1000维，hidden layer 有1000个 nodes，output layer 为1个 node，则它的 VC维大约为 O(1000*1000)。可以看到，神经网络的 VC维相对较高，因而它的表达能力非常强，可以用来处理任何复杂的分类问题。根据上一节的结论，要充分训练该神经网络，所需样本量为10倍的 VC维，所以所需数据量是一个巨大的数字。如此大的训练数据量，在20世纪，训练出的复杂神经网络模型的泛化能力不是很好，容易过拟合。但现在为什么深度学习的表现越来越好。原因是多方面的，主要体现在：

通过修改神经网络模型的结构，以及提出新的 regularization 方法，使得神经网络模型的VC维相对减小了。例如卷积神经网络，通过修改模型结构(局部感受野和权值共享)，减少了参数个数，降低了 VC维。2012年的AlexNet，8层网络，参数个数只有60M；而2014年的GoogLeNet，22层网络，参数个数只有7M。再例如dropout，drop connect，denosing 等 regularization 方法的提出，也一定程度上增加了神经网络的泛化能力；
训练数据变多了。随着互联网的越来越普及，相比于以前，训练数据的获取容易程度以及量和质都大大提升了。训练数据越多，E-in 越容易接近于 E-out。而且目前训练神经网络，还会用到很多 data augmentation 方法，例如在图像上，剪裁，平移，旋转，调亮度，调饱和度，调对比度等都使用上了；
除此外，pre-training 方法的提出，GPU 的利用，都促进了深度学习。

但即便这样，深度学习的 VC维和VC界依旧很大，其泛化控制方法依然没有强理论支撑。但是实践又一次次证明，深度学习是好用的。所以 VC维对深度学习的指导意义，目前不好表述，不好表述就绕过它不表述，其中一个这么想的就是大牛 LeCun，他对 SVM 和 VC 理论没那么看重，《KDnuggets Exclusive: Interview with Yann LeCun, Deep Learning Expert, Director of Facebook AI Lab》这篇对 LeCun 的访谈里 LeCun 表达出的观点很直接暴力：

承认 SVM 和 VC理论很不错，但深度神经网络的 VC 维也是有限的，所以也是有 VC 界的，虽然 VC维和 VC界确实都有点大；
SVM 只是一个第一层是度量支持向量和输入相似性、第二层是组合这些相似性的双层系统，其中第一层使用最简单的无监督学习方法，即直接使用训练样本来构建类别簇，有点简单了，虽然 SVM 的 VC理论能够以漂亮的数学方法进行容量控制（Capacity Control，指的是一种可学习性吧），容量控制能力虽然也重要，但没有表达能力重要，比如 SVM 不具备对图像的 “偏移、缩放、旋转、光照、背景杂乱” 等不变性，而这对于卷积神经网络来说很容易。

虽然有 “位置决定想法” 的嫌疑，但不得不说也有一定道理。但就现状而言，PAC 可行性分析和 VC理论仍然是机器学习理论分析最重要的理论基础。

八、应用示例

回到最开始的问题，“对于一个任务，我准备使用的机器学习方法是否合理、数据量至少需要多少，这些问题如何在进行实验之前就能被解答？”。下面分别从 VC维和数据量的选择分别说一下。

VC维的选择

将原 VC界不等式稍作改写，那么在很高的概率下，模型的泛化误差和训练误差满足如下式子，

$E_{out}(h)\leqslant E_{in}(g)+\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta })}$

上式第3项表示了模型的复杂程度，可以看到是关于 VC维的递增函数，所以 VC维越大，两者差别越大。又由于我们知道，VC维越大，模型表达能力越强，模型的训练误差越小。模型相关性能如图4所示，

图4 模型的泛化误差、训练误差、模型容量随 VC维变化示意图

E-out - E-in 和 E-in 的下降速度在每个阶段都是不同的，因此我们需要寻找一个二者兼顾的 VC维，来保证 E-out 最小。

数据量的选择

面对一个这样的问题：针对2维数据，做一个2分类任务，泛化误差和训练误差的最大差距允许是 0.1，对应置信度是 90%，所用的模型是线性分类模型，需要多少数据？

首先，对于2维数据的线性二分类任务，d_vc=3，由于有 ε=0.1，δ=1-90%=0.1，然后经过下面一番估算，

于是我们知道了，需要29300条训练数据作为训练集。从上面这个例子，可以看到 VC维对于训练数据量的选取具有很直观的指导意义。

事实上，对于一般情况，VC维越大，需要更多的训练数据。理论上，数据规模需要满足 N=10000d_vc；但实际经验是只需要满足 N=10d_vc。造成理论值与实际值之差如此之大的最大原因是，VC界为了保证其泛化正确性，推导过程中过于宽松了：

将 Hoeffding不等式应用在 “任何数据分布、任何假设空间” 上；
有效假设数 m-H 设定成与 N 相关的函数，与具体数据无关，而事实上训练样本并不是任意 N 个；
同一个 VC维的值可以各种各样的假设空间，而实际应用时假设空间是固定的一类函数；
推导出的 VC界是最坏情况下的上界，即与学习策略和算法无关，而实际应用时我们会先验地去选择一个合适的策略和算法。

因为 VC界对数据分布 D、目标函数 L、备选函数集 H、学习算法 A 都没有要求，它牺牲了部分精确性，换来了无所不包的一般性，这使得 VC界具备一定程度上的指导性，毕竟实际应用时还有 ”具体问题具体分析“ 和 ”效果好就是好“ 两板斧。即便如此，就目前来说，VC维 & VC界依然是分析机器学习模型的最重要的理论工具。

参考文献

机器学习 · 总览篇 X