本篇章是监督学习篇,本文作为监督学习篇的第一篇文章,主要是对监督学习进行概括性介绍。
算法。文章首发于我的博客,转载请保留链接 ;)
总览篇介绍完后,接下来就是在监督学习、深度学习、强化学习、无监督学习、半监督学习中选一个主题作为第二个大篇章,首先深度学习跟其它四类不在一个位面上:深度学习是根据模型的结构上的差异化形成的机器学习的一个分支,而其它四类是连接主义学习的四大类别,深度学习跟四类都是有都分重叠关系,如图1所示。
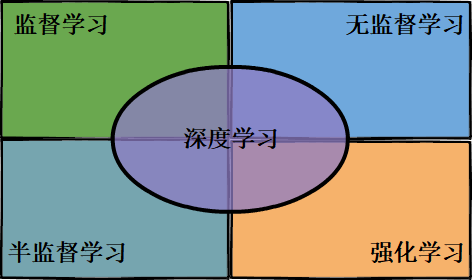
对于以上五个主题,无论是从知识广度还是应用范围来排优先级都不好排,思来想去还是结合 “领域热度”、“历史发展顺序”、“知识延展顺序” 这三个方面来排篇章的主题顺序:监督学习(发展最早、热度较高)、深度学习(热度最高)、强化学习(热度较高)、无监督学习(基础知识)、半监督学习(延展知识)。所以本篇章的主题是 “监督学习”。
传统的机器学习分类中通常是:监督学习(Supervised learning) 和无监督学习(Unsupervised learning),还有一种结合监督学习和无监督学习的中间类别,称之为半监督学习(Semi-supervised Learning)。传统的机器学习分类没有提到过强化学习,而在连接主义学习(源于仿生学)中,把强化学习(Reinforcement learning) 作为与以上三类方法并列的一类机器学习方法,个人认为可以把强化学习看成是一种通过环境内部产生样本(特征和标签的匹配对)的监督学习。
监督学习和无监督学习很好区分:是否有监督(supervised),就看输入数据是否有标签(label),输入数据有标签,则为有监督学习,没标签则为无监督学习。 一个话糙理不糙的例子是:你小时候见到了狗和猫两种动物,有人告诉你这个样子的是狗、那个样子的是猫,你学会了辨别,这是监督学习;你小时候见到了狗和猫两种动物,没人告诉你哪个是狗、哪个是猫,但你根据他们样子、体型等特征的不同鉴别出这是两种不同的生物,并对特征归类,这是无监督学习。监督学习、半监督学习、无监督学习关于数据标注完整度的比较大致可如图2表示,

图2中,监督学习的数据都是有确定标注的;半监督学习使用 “有标签数据+无标签数据” 混合成的数据;半监督聚类里数据即使有标签,也都是不是确定性的,举个例子,标签可能是 “不是 C 类”,或者是 “A、B 两类中的一类” 这种形式;而无监督学习使用的数据完全是没有标签的。
本文是《监督学习篇》的第一篇文章,下面将概括性地介绍监督学习包含了哪些常用算法,以及各种算法的特点和适用场景。
一、监督学习模型
如《总览篇 V》中所述,模型通常有两种分类方式:第一种是按模型形式分类:概率模型(Probabilistic Model)和 非概率模型(Non-probabilistic Model);第二种是按是否对观测变量的分布建模分类:判别模型(Discriminative Model)和 生成模型(Generative Model)。这两种分类方法事实上把所有模型划分成了三类,可用图3清楚地表示,

模型一共分为图中的三种模型:非概率模型(Non-probabilistic Model)、概率判别模型(Probalilistic Discriminative Model)、生成模型(Generative Model);三种模型挖掘信息的程度从少到多,解决问题的途径从直接到间接。其中,每种类别的代表性模型如下:
I. 非概率模型,直接判别:感知机(单层神经网络,Perceptron)、多层感知机(MLP)、支持向量机(SVM)、K近邻(KNN)
II. 概率判别模型,间接利用条件概率判别:逻辑回归(LR)、决策树(DT)、最大熵模型(ME)、条件随机场(CRF)
III. 生成模型,更间接地先求联合概率,然后利用贝叶斯定理判别:高斯判别分析(GDA)、朴素贝叶斯(NB)、受限玻尔兹曼机(RBM)、隐马尔科夫模型(HMM)
二、如何选择合适的监督学习算法
这么多种监督学习算法,如何选择合适的算法?这个问题的答案取决于许多的因素,其中包括:
- 数据值的形式,连续还是离散;
- 数据的维度,大还是小;
- 数据量,多还是少;
- 可以利用的计算资源,CPU或者GPU的计算能力;
- 对模型准确性和效率的要求。
- 对模型可解释性的要求。虽然学习如何权衡输入变量的复杂组合能够带来更准确的预测,但它也使得解释机器学习模型变得更困难。可被解释的预测模型生成的决策,是由原始输入变量带来的,而不是输入变量的任意高阶组合、缩放、加权组合带来的,所以对特征进行操作越直观的模型可解释性越强。
通过对以上因素的分析,我们可以选择一个直观上比较合适的模型进行建模。那么具体如何利用这一先验知识,指导我们去选择合适的算法模型,帮助我们少走一点弯路呢?下面图4是一个比较经典的算法选择流程图,

这张图我只是起到一个 “翻译+搬运工” 的作用,此图来源于 Microsoft Azure。首先毫无疑问,我们可以根据数据值的因变量,或者称之为标签,是连续值还是离散值,将监督学习问题分为分类问题和回归问题,其中分类问题的标签是离散值,回归问题的标签是连续值。但是往后的节点,比如根据 准确率和效率、可解释性、数据量 等指标对算法进行取舍,我个人认为本图给的后续选择流程图过于宽泛了,只具备有限的参考价值。本文下面将从更细致的角度对各个算法进行分析。
| 类型 | 训练时间复杂度 | 预测时间复杂度 | |
|---|---|---|---|
| 支持向量机 | 非概率判别模型 | ||
| K近邻 | 非概率判别模型 | ||
| 神经网络 | 非概率判别模型 | ||
| 逻辑回归 | 概率判别模型 | ||
| 决策树 | 概率判别模型 | ||
| 朴素贝叶斯 | 生成模型 | ||
| 高斯判别模型 | 生成模型 |
上述表格,对于训练和预测时间复杂度两列中,N 是训练样本数,M 是样本特征维度,其中支持向量机的 是支持向量的个数,神经网络的 P 是网络参数总个数,K近邻表格中时间复杂度对应的方法是KD树法,决策树的 D 是决策树的层数;另外需要注意,涉及到迭代法优化问题的模型,比如神经网络、逻辑回归等,它们的训练时间复杂度都是按照每个样本迭代常数次计算的。
我们结合上述表格,一一分析各个模型的特点:
- 支持向量机,训练时间复杂度太高,这意味着样本数目太高训练效率很低;而且最后起作用的支持向量数目也是有限的,这意味着在特征维度一定的情况下,过多的训练样本数对模型预测准确率的提升也不大。所以综合两点,支持向量机适合小规模数据集。
- K近邻,没有显式的训练过程,它的特点是完全跟着数据走,没有数学模型可言,也正因为如此具有很强的可解释性。表格中给的是 KD 树实现的时间复杂度,如果是朴素方法,训练时间复杂度更低一点,是 O(N M),但预测时间复杂度高达 O(N logK),效率极低。即使使用 KD 树实现,当特征维度稍微大一点,效率也是极低;所以K近邻法特征维度一般不超过20,实用价值严重受限。
- 神经网络,这里是以多层感知机(MLP)为例,现在深度学习层数和节点数目通常都比较大,所以网络参数个数P一般很大,P越大意味着越强的函数拟合能力,但前提是足够的计算资源和训练数据,所以说神经网络的表现效果一定程度上取决于计算资源和数据量。
- 逻辑回归,训练和预测效率都很高,多维输出时的Softmax层通常作为现在深度学习的最后一层,使用广泛,效果也良好。
- 决策树,决策树每个节点有十分具体的物理意义,所以有很强的解释性,训练效率较快,当我们希望能更好地理解手头数据的时候,往往可以使用决策树。但也是受限于其简单性,决策树更大的用处是作为一些更有用的算法的基石,比如随机森林,还有 BAT、华为等公司大数据比赛 几年前流行的算法 GBDT,和最近几年流行的算法 XGBoost。
- 朴素贝叶斯,跟K近邻类似,也没有显式的训练过程,因此也有较强的可解释性,这一点与图4结论不太一样哈。训练和预测效率效率都很高。典型的应用场景就是垃圾邮件过滤器,效果一般会很好。
- 高斯判别模型,高斯判别模型是基于伯努利分布的,这一点与逻辑回归一致,事实上高斯判别模型求得的后验概率跟逻辑回归的函数形式也是一致的,差别就在于高斯判别模型多一个对各个类别数据本身的分布假设——高斯分布,这意味着高斯判别模型比逻辑回归需要更加严格的模型假设,在实践中,逻辑回归比高斯判别模型的泛化性能更强。除此之外,计算过程需要求 “特征X” 减 “特征期望” 的协方差矩阵,所以效率会比逻辑回归低一点。
总的来说,就像机器学习领域中惯用的一句话,没有最好的模型,只有最合适的模型,这句话很zhengzhi正确。但我认为,就实际应用的准确率来看,深度神经网络 > 支持向量机 > 其它,另外有一些像英语老师常说的 “固定搭配、死记住” 的一些适合特殊场景的算法,比如 垃圾邮件过滤器——朴素贝叶斯模型,类别性质的稀疏特征——逻辑回归模型,大数据推荐算法——XGBoost 等经验性质结论,不一定完美,但效果一定不错。
本文是《监督学习篇》的第一篇文章,也是概括性地介绍了一下各种广泛使用的监督学习方法的特点和适用场景,在《监督学习篇》后续的文章中会详细地对每一种监督学习方法进行更深入地介绍,包括不使用机器学习相关工具包的算法代码实现示例。
参考文献
- 《统计学习方法》 李航
- Stanford CS 229 ― Machine Learning
- wiki: 朴素贝叶斯分类器
- wiki: 决策树
- zhihu:什么是无监督学习?
- cnblogs:支持向量机(五)SMO算法
- jianshu:基础-12:15分钟理解KD树
- csdn: 斯坦福大学机器学习——高斯判别分析