在机器学习中,朴素贝叶斯分类器是一系列以假设特征之间强(朴素)独立下,运用贝叶斯定理为基础的简单概率分类器。朴素贝叶斯模型虽然简单,但仍然是文本分类的一种热门(基准)方法。
算法。文章首发于我的博客,转载请保留链接 ;)
对于文本相关分类任务,比如过滤恶意留言、过滤垃圾邮件等任务,一种十分常用的方法就是使用朴素贝叶斯分类模型。本文将会从基本原理、代码实现、应用等角度详细介绍朴素贝叶斯模型。
一、基本原理
贝叶斯这个名字很多人都知道或者有所耳闻,统计学上有一个耳熟能详的贝叶斯学派和贝叶斯定理:关于贝叶斯学派的详细介绍可参见本专题的 《总览篇·III 统计推断: 频率学派和贝叶斯学派》 一文;而贝叶斯定理是上学时可能会接触到的,内容是,对于事件 A、B,假设其发生概率为 P(A)、P(B),则有,
这个定理最大的作用就是告诉我们 A、B 两个事件之间后验概率的关系和转化方式。
贝叶斯定理在机器学习中应用最广泛的就是朴素贝叶斯模型(Naive Bayesian Model,NBM)。朴素贝叶斯模型发源于古典数学理论有着坚实的数学基础,是本文主要介绍的内容。朴素贝叶斯,之所以称之为 “朴素”,是因为其中引入了几个假设,而正因为这些假设的引入,使得模型简单、朴素、易理解。
现在我们对朴素贝叶斯模型的公式进行推导。首先,命
其中(1)式中 x 是待分类样本,每个 a 是 x 的一个特征属性;(2)式中 C 是类别集合。分类任务目标是在样本出现 x 特征情况时,判别该样本最有可能是属于哪一类,朴素贝叶斯模型做法很直接,它先计算该样本属于每个类别的后验概率,
求得(3)式中样本属于各个类别的后验概率后,选择后验概率最大的类别作为样本分类类别。所以现在的关键点就是如何计算(3)式中的各个条件概率,这个时候就需要用上贝叶斯定理,
其中 P(x) 表示的是样本呈现出 x 的特征形式的概率,这个概率通常会看成一个常数,所以我们的目的是求(4)式中分子最大对应的类别 i,而分子都是可以直接求出的量。但问题是 x 作为多个维度特征组成的特征向量,本身在训练参考样本中出现的次数就不会太多,各个类别的 出现的次数就更少了,这样得到的概率值意义不大,所以直接求这个后验概率没什么用。但我们发现 x 的每个属性 a 出现的次数会多很多,所以这里为了让分类模型能够 work,就要引入朴素贝叶斯假设了,即认为各个特征属性 a 都是互相独立的,那么将(4)式分子部分中
展开有,
所以总的来说,朴素贝叶斯模型要做的事情就只是统计一下各个类别 y 下的各个 a 出现的概率,以及类别 y 本身出现的概率,就可以对新样本 x’ 进行分类了。
从上述公式推导过程中可以看到,朴素贝叶斯不同于其它模型,没有复杂的优化过程,所需估计的参数也很少,效率极高,对缺失数据不太敏感,理论上,朴素贝叶斯分类模型与其他分类方法相比具有最小的误差率;但由于各个特征属性 a 都是互相独立的这一朴素假设在实际应用中往往是不成立的,朴素贝叶斯分类效果并没有理论上的那么完美。
二、Python 实现
如文章开头所述,一个典型的朴素贝叶斯模型应用场景是垃圾文本过滤,本小节就只用 numpy 库手写实现手机短信垃圾(SMS Spam)分类,选用的数据集是经典的 SMS Spam Collection v. 1,共5,574条短信,其中垃圾短信747条,非垃圾短信4827条。“SMS Spam Collection v. 1” 数据集格式如下所示,
1. ham MY NO. IN LUTON 0125698789 RING ME IF UR AROUND! H*
2. ham Siva is in hostel aha:-.
3. spam FreeMsg: Txt: CALL to No: 86888 & claim your reward of 3 hours talk time to use from your phone now! ubscribe6GBP/ mnth inc 3hrs 16 stop?txtStop
4. ham Cos i was out shopping wif darren jus now n i called him 2 ask wat present he wan lor. Then he started guessing who i was wif n he finally guessed darren lor.
5. spam Sunshine Quiz! Win a super Sony DVD recorder if you canname the capital of Australia? Text MQUIZ to 82277. B
每个样本一行,上面的示例一共有5个样本。1、2、4属于正样本,即正常消息,标签是”ham”;3、5属于负样本,即广告等垃圾消息,标签是”spam”。标签后面就是具体的消息内容。
2.1 不使用机器学习库的 numpy 实现
首先是不使用机器学习库的实现,主要包括 特征提取、训练、预测 三个过程。
2.1.1 特征提取
特征提取的第一步是将句子切分成单词,由于是英文,所以这里处理方式比较简单暴力,按照空格和除’之外的符号来切分了,然后全部转小写。为了选出可以作为特征的单词,可以统计单词出现的文档次数,并试图把直观上无效(出现在的文档数目较少)的单词排除掉,当然了,也可以把所有单词都作为特征,这里只是想尝试一下。统计结果如下图1所示,
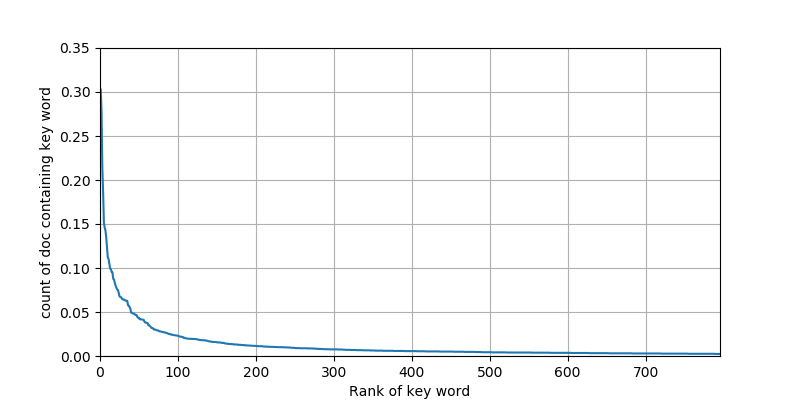
共有7956种单词出现,图1表明了绝大部分单词出现频次都相当低。后文中,我们分别选取了前 200、500、2000、5000、7956 这5种截断方式来作为特征,特征维度对应的就是 200、500、2000、5000、7956 维。
2.1.2 训练
朴素贝叶斯没有显式的训练过程,所谓的训练过程只是计算以下参数:样本类别在样本中出现的先验概率 和 “关键字|类别” 的条件概率。以上的参数就是模型的全部参数,是可以直接从训练样本计算得到的,没有最优化过程。下面是相当朴素的 python 实现代码,就只是在计算 P(类别) 和 P(关键字|类别)。
class NaiveBayesClassificationModel(object):
"""
朴素贝叶斯模型
"""
def __init__(self, kw_set):
# 关键字集合,即哪些单词是我们要当做是特征属性的单词
self.kw_set = kw_set
# P(类别) 样本类别本身在样本中出现的先验概率
self.label_prior_prob = dict()
# P(关键字|类别) 这一条件概率
self.kw_posterior_prob = dict()
def train(self, data):
"""
训练模型
:param data: 以 [[label] [input_text_words]] 的形式构成的list
:return: None
"""
# 计算条件概率 P(关键字|类别)
for label, input_text_words in data:
if label not in self.kw_posterior_prob:
self.kw_posterior_prob[label] = dict()
if label not in self.label_prior_prob:
self.label_prior_prob[label] = 0
self.label_prior_prob[label] += 1
for word in input_text_words:
if word not in self.kw_set:
continue
if word not in self.kw_posterior_prob[label]:
self.kw_posterior_prob[label][word] = 0
self.kw_posterior_prob[label][word] += 1
for label, kw_posterior_prob in self.kw_posterior_prob.items():
for word in self.kw_set:
if word in kw_posterior_prob:
self.kw_posterior_prob[label][word] /= self.label_prior_prob[label] * 1.0
else:
self.kw_posterior_prob[label][word] = 0
# 样本类别本身在样本中出现的先验概率 P(类别)
for label in self.label_prior_prob:
self.label_prior_prob[label] /= len(data) * 1.0
2.2.3 预测
预测过程也相当简单,实现这个式子即可,
下面就是简单的 python 代码实现,
def predict(self, input_text):
"""
预测过程
:param input_text: 处理过后的单词集合
:return:
"""
predicted_label = None
max_prob = None
for label in self.label_prior_prob:
prob = 1.0
for word in self.kw_set:
if word in input_text:
prob *= self.kw_posterior_prob[label][word]
else:
prob *= 1 - self.kw_posterior_prob[label][word]
if max_prob is None or prob > max_prob:
predicted_label = label
max_prob = prob
return predicted_label
完整代码可见 github: https://github.com/KangCai/Machine-Learning-Algorithm/blob/master/naive_bayes.py
2.2 scikit-learn 实现
上一小节 2.1 中采用的实现方式是:某个单词在文档中出现过,则其特征值为1,否则为0,所以实际采用的是 BernoulliNB 伯努利模型。scikit-learn 具体实现如下
from sklearn.naive_bayes import BernoulliNB
# 针对本例子,使用 BernoulliNB Naive Bayes;
bnb = BernoulliNB()
bnb.fit(X, Y)
result_predict = bnb.predict(X')
与伯努利模型一样,MultinomialNB 多项式模型 同样是适用于离散特征的情况,两者实现上的差别在于,在计算条件概率时,多项式模型的特征取值不是1或0,即不仅仅是出现与否,还需要考虑出现次数。除此之外 skikit-learn 还提供第三种模型 GaussianNB 高斯模型,它是用来解决特征是连续变量的情况的,高斯模型与多项式模型在实现上唯一不同的地方就在于,计算条件概率时,高斯模型假设各维特征服从正态分布,需要计算的是各维特征的均值与方差。
2.3 交叉验证结果
通过 2.1 的代码实现,做4折-交叉验证,准确率为
| 200 | 500 | 2000 | 5000 | 7956 | |
|---|---|---|---|---|---|
| 准确率 | 97.5% | 97.9% | 97.0% | 95.7% | 95.5% |
| 时间(秒) | 0.3 | 0.6 | 2.5 | 4.7 | 4.9 |
从上表可以看到,特征维度越高,即参考的单词越多,耗时也会随之线性增加,而准确率没有呈增加趋势的,在特征维度为500时达到最大准确率97.9%。
另外,为了进一步地研究朴素贝叶斯模型针对垃圾消息分类任务的适用性,下面列出了当特征维度为 5000 时的混淆矩阵,
| 判成正常 | 判成垃圾 | |
|---|---|---|
| 正常 | 99.2% | 0.8% |
| 垃圾 | 12.9% | 87.1% |
朴素贝叶斯模型的参数没有最优化过程,参数是直接获取的,这使得模型创建过程简单、可解释性强。相比于其它模型,朴素贝叶斯模型在文本(包括广告、政治敏感、赌博、色情、违法犯罪等)分类任务上有很大的竞争力。