K近邻(k-Nearest Neighbor,KNN)分类算法,是一种很 “直白” 的算法,由美国学者 Cover 和 Hart 于1968年在 IEEE 发表。该算法算法思路很简单,对于一个样本的类别判定,只需要在特征空间中找与它最相似的 K 个样本,这些样本大多数属于哪一类别,该样本就判定成哪一类别。
文章首发于我的博客,转载请保留链接 ;)
一、概念
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一种很 “直白” 的算法,它的算法思路是,对于一个样本的类别判定,只需要在特征空间中找 与它最相似的 K 个样本,这些样本大多数属于哪一类别,该样本就判定成哪一类别,以下图的情况为例,
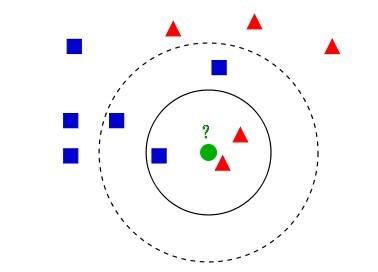
,对于绿色原点,如果选择K=3,即选择实线圈范围内,那么离绿色点最近的有2个红色三角形和1个蓝色的正方形,用这3个点投票, 于是绿色的这个待分类点属于红色的三角形;如果选择K=5,即选择虚线圈范围内,那么离绿色点最近的有2个红色三角形和 3个蓝色的正方形,用这5个点投票,于是绿色的这个待分类点属于蓝色的正方形。
我们可以看到,KNN 本质是一种基于数据统计的方法。这种方法没有显式的前期训练过程,而是在预测时把数据集加载到内存后,根据 数据样本来进行分类,我们也称之为 memory-based learning,或者 instance-based learning。朴素贝叶斯模型与 KNN 在这一点上很相似,也是没有显式的训练过程。
与 KNN 算法容易弄混淆的是 K-Means 算法,但两者其实只有一点点共性,
KNN 与 K-Means 的区别
| KNN | K-Means | |
|---|---|---|
| 类型 | 监督学习、分类 | 无监督学习、聚类 |
| 训练过程 | 无显式 | 显式 |
| k的含义 | 预测阶段分类参考的样本数目 | 训练阶段聚类的类别数 |
KNN 与 K-Means 的共性
两种算法的实现过程中,都包含了一个 “给定一个点,在数据集中找到离它最近的点” 的计算过程,即两者都用到了近邻算法, 如果数据集很大且寻求高效的话一般用 KD 树来实现近邻算法。
二、算法步骤
根据实现方式的不同,将 KNN 分为 “朴素实现” 和 “KD树实现”,假定训练数据量为 N。
2.1 朴素实现
1.计算测试数据与各个训练数据之间的距离;复杂度为 O(N);
dist = np.linalg.norm(X_val[i, :] - self.X_train, axis=1)
2.选取距离最小的 K 个点;利用最大K-堆排序,一般认为复杂度为 O(NlogK),然而实际平均复杂度为 O(N + KlogK),这个需要推导一下;
# 1. 直接从小到大排序 O(NlogN)
res_idx = np.argsort(dist)[:self.k]
res = [self.Y_train[i] for i in res_idx]
# or 2. 最大堆排序 O(NlogK)
heap = []
for idx, d in enumerate(dist):
if len(heap) < self.k:
heapq.heappush(heap, (-d, idx))
elif d < -heap[0][0]: # -heap[0][0] is the maximum distance in heap.
heapq.heappushpop(heap, (-d, idx))
res = [self.Y_train[r[1]] for r in heap]
3.确定这 K 个点所在类别的出现频率,选择频率最高的分类作为测试数据的类别;复杂度为 O(K);
label = np.argmax(np.bincount(res))
所以最后,由于没有训练过程,故训练复杂度是 O(1),测试复杂度是 O(N + KlogK)。
2.2 KD树实现
1.为训练数据建立 KD 树;复杂度为 O(N(logN)^2);
// Create KD tree.
kd_node = _create_kd_tree(point_container_list, col)
// DFS
def _create_kd_tree(self, points, dim, i=0):
if len(points) > 1:
points.sort(key=lambda p: p.x[i])
i = (i + 1) % dim
half = len(points) >> 1
return self._create_kd_tree(points[:half], dim, i), self._create_kd_tree(points[half+1:], dim, i), points[half]
elif len(points) == 1:
return None, None, points[0]
2.选取距离最小的 K 个点,这里的 K 与 KD树 的 K 含义不同,KD树 中的 K 表示的是数据维度;利用 KD树 的搜索,平均复杂度为 O(logN),当然,最坏复杂度会比较高;
// Seach nearest neighbor in KD tree.
_search_kd_tree(kd_node, p, k, dim, lambda a, b: sum((a[i] - b[i]) ** 2 for i in range(dim)))
// DFS
def _search_kd_tree(self, kd_p, p, k, dim, dist_func, i=0, heap=None):
import heapq
is_root = not heap
if is_root:
heap = []
if kd_p and isinstance(kd_p, tuple) and len(kd_p) == 3:
mid_kd_p = kd_p[2]
dist = dist_func(p.x, mid_kd_p.x)
dx = mid_kd_p.x[i] - p.x[i]
if len(heap) < k:
heapq.heappush(heap, (-dist, mid_kd_p))
elif dist < -heap[0][0]: # -heap[0][0] is the maximum distance in heap.
heapq.heappushpop(heap, (-dist, mid_kd_p))
i = (i + 1) % dim
self._search_kd_tree(kd_p[dx < 0], p, k, dim, dist_func, i, heap)
if dx * dx < -heap[0][0]: # -heap[0][0] is the maximum distance in heap.
self._search_kd_tree(kd_p[dx >= 0], p, k, dim, dist_func, i, heap)
if is_root:
nn_result = sorted((-h[0], h[1]) for h in heap)
return [n[1] for n in nn_result]
3.最后一步与朴素实现一样,确定这 K 个带你所在类别的出现频率,选择频率最高的分类作为测试数据的类别;复杂度为 O(K);
label = np.argmax(np.bincount(res))
所以最后,训练复杂度是 O(NlogN),测试复杂度是 O(KlogN),可以看到,当 k « N 时,测试性能比朴素实现高很多。
KNN 完整代码见 https://github.com/KangCai/Machine-Learning-Algorithm/blob/master/k_nearest_neighbor.py
KDTree 完整代码见 https://github.com/KangCai/Machine-Learning-Algorithm/blob/master/util_kd_tree.py
三、三种实现的表现效果
比如对于一个很简单的场景,
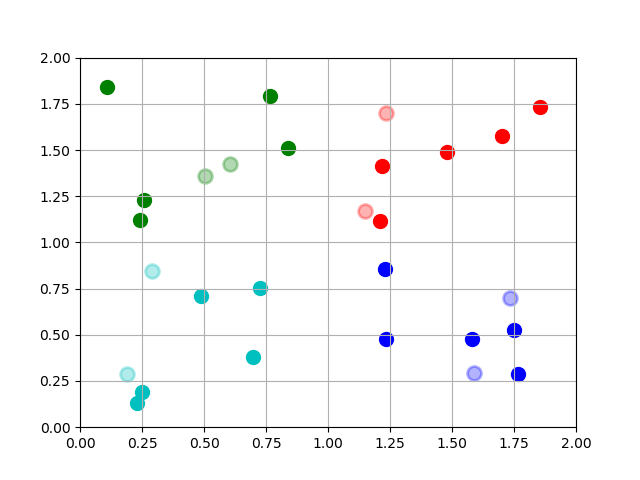
如图,4 种不同颜色的点表示 4 个类别,其中深色的点是训练样本,浅色的点是测试样本,浅色点的外环颜色表示分类结果,近邻数 k 取的是 5, 可以看到 8 个浅色的点全部分类正确。
三种不同实现方法的 KNN 的分类结果是一致的,下面来比较三种实现的效率高低,设搜索近邻数为 k,训练样本数 n,测试样本数 m,特征维度 d, 用第二章所述的方法测试,耗时如下(单位秒 s),
| Naive | Heap | KDTree | |
|---|---|---|---|
| 5-100000-200-2 | 2.5 | 6.0 | 0.05 |
| 5-100000-10-100 | 0.9 | 1.0 | 65.4 |
| 1000-100000-200-2 | 2.5 | 6.8 | 3.4 |
| 1000-100000-10-100 | 0.9 | 1.0 | 65.4 |
| 5-1000-200-2 | 0.02 | 0.06 | 0.04 |
| 5-1000-200-500 | 0.78 | 0.78 | 60.9 |
根据上述结果,作出以下分析和结论,
- 根据 Naive列 和 Heap列 的横向比较分析:理论上,Heap 相比于 Naive 方法肯定要快,实验结果之所以相反,是由 Naive 是借助 numpy 实现,而 Heap 没有;
- 根据 KDTree列 纵向分析:对于 KDTree 来说,特征维度 d 影响最大(指数),近邻数 k 有一定影响(线性),训练样本数 n 对分类影响很小(主要是影响创建效率)
- 分别根据 Naive列 和 Heap列 的纵向比较分析:对于 Naive 和 Heap 实现来说,特殊维度 d 有一定影响(线性),训练样本数 n 也有一定影响(略高于线性)
综合以上分析,应用场景如果特征维度 d 较小(<20),KNN 适合用 KDTree 实现;如果训练样本数 n 较小 (<100000),KNN 适合用朴素方法实现。
除此之外,如果借助 scikit-learn 实现,老样子,可以几行搞定,
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier()
knn.fit(X, Y)
result_predict = lr.predict(X')
参考资料