算法。文章首发于我的博客,转载请保留链接 ;)
变换矩阵
1.位移(Translation) 对于一个三维坐标(x, y, z),我们想让它往x轴正方向移动1个单位,往y轴正方向移动1个单位,往z轴正方向移动1个单位,则可以让它加上一个向量(1, 1, 1)
2.旋转(Rotation) 对于一个三维坐标(x, y, z),点(x, y, z)绕轴(u, v, w)旋转θ的矩阵是如下所示,
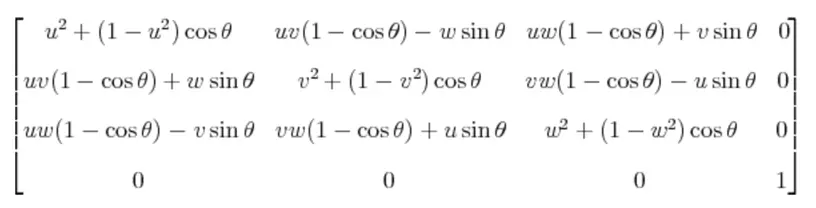
3. 缩放(Scale) 对于一个三维坐标(x, y, z),我们想让它扩大2倍,则可以让它变成(2x, 2y, 2z)。写成矩阵乘法的话,V2 = M*V1,M如下图:

4.通用

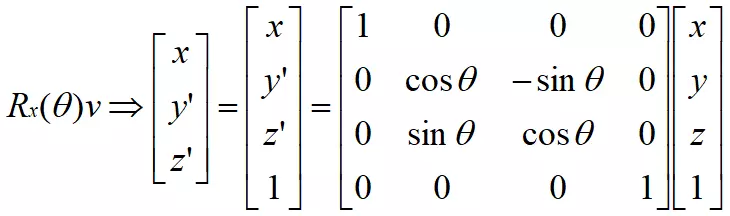

5.性质
旋转和缩放矩阵可交换(communicative) 先旋转后缩放和先缩放后旋转的结果是一样的。RS = SR。 位移不满足交换律 先位移再旋转和先旋转再位移结果是不一样的!因为旋转之后模型的正面朝向就变了,所以会向新的方向位移。 TS!=ST, TR!=RT。
对于任何一个线性变换矩阵,我们可以把它拆解(decompose)为TRS或TSR三个矩阵的乘积的形式。1)首先提取最后一列,得到位移。2)剩余的矩阵是R和S相乘的矩阵
坐标系
3D物体从三维坐标映射到2D屏幕上,要经过一系列的坐标系变换,这些坐标系如下:
1.model 物体本身(local)的坐标系,是相对坐标。 比如一个3D人物模型,头部某个点的坐标为(0,0,20),这是相对该模型的中心点(0,0,0)说的。当模型向前移动了5个单位,其中心点依旧是(0,0,0),头部那个点依旧是(0,0,20)
2.world 世界坐标系,即物体放在世界里的坐标,也就是大家最能理解的那个坐标。 还是上面的例子,他沿Z轴移动了5个单位后,中心点在世界坐标里变成了(0,0,5),头部那个点变成了(0,0,25)。 物体的位移,缩放,旋转会改变它的世界坐标,不会改变它的model坐标。
3.image 相机坐标系。 相机也是世界里的一个物体,相机坐标就是以相机位置为坐标原点,相机的朝向为Z轴方向的坐标系。因为我们在电脑里看到的物体其实都是“相机”帮助我们看的,“相机”就是我们的眼睛,所以要以相机为标准进行坐标转换。 在model,world,image坐标系下,X,Y,Z的范围都是无穷大,只是坐标系的基准不一样而已。
4.perspective (NDC, Normalized Device Coords) 透视坐标系。 这一步是将三维坐标向二维平面进行映射,经过透视变换之后,(x, y)的范围在[-1, 1],z的范围在[0, 1] 可能有点难以理解,本文后面会有专门解释。
5.screen 屏幕坐标系。 因为屏幕是有分辨率的,比如1920×1080,所以还要再进行一次变换。 该坐标系的原点在屏幕左上角,x轴朝右,y轴朝下。x的范围在[0, xres-1],y的范围在[0, yres-1],即x是[0, 1920),y是[0, 1080)。 z值是[0, MAXINT],z=0就是屏幕那个平面,z=MAXINT就是无穷远。
坐标系的变换矩阵
1.从model变到world。 从模型本身的相对坐标变换到世界坐标,就是平移,旋转,缩放。
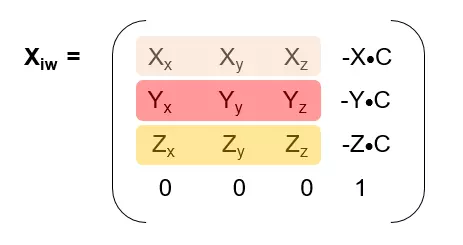
2.从world变到image(相机坐标)。 这一步是将物体在世界的坐标转换为相对相机的坐标。 首先要计算出相机的坐标系: 相机也是世界里的物体,我们假定相机的中心点在世界里的位置是C(Cx, Cy, Cz) 相机正在看着某个方向,我们假定相机正在看的点的位置是I(Ix, Iy, Iz) 那么,相机的 Z 轴就是它看的方向的向量,即CI向量,也就是I-C=(Ix-Cx, Iy-Cy, Iz-Cz),标准化之后就得到了 Z。接下来就是求 X 和 Y。
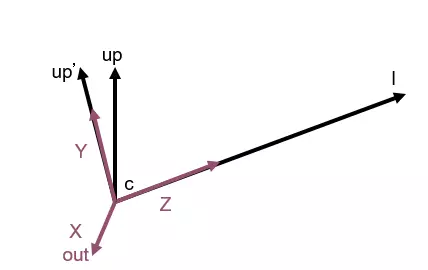
然后我们取世界坐标系里的up向量(0,1,0)。通过up叉乘Z(注意顺序),我们可以得到一个向量X1,将X1标准化(即使其模为1),我们就得到了 X 轴的单位向量。 在通过Z轴的单位向量与X轴的单位向量叉乘,即 Z×X(注意顺序),我们就得到了Y轴的单位向量。 然后计算变换矩阵: 根据方程组来解,世界坐标系中,相机原点为(Cx, Cy, Cz),在相机坐标系中为(0,0,0)所以,(0, 0, 0) = Xiw *(Cx, Cy, Cz),世界坐标系中,相机的三个轴为X+C=(Xx+Cx, Xy+Cy, Xz+Cz), Y+C=(Yx+Cx, Yy+Cy, Yz+Cz), Z+C=(Zx+Cx, Zy+Cy, Zz+Cz),但在相机坐标系下为(1,0,0),(0,1,0),(0,0,1) 所以 ,(1, 0, 0) = Xiw *(Xx+Cx, Xy+Cy, Xz+Cz); (0, 1, 0) = Xiw *(Yx+Cx, Yy+Cy, Yz+Cz); (0, 0, 1) = Xiw *(Zx+Cx, Zy+Cy, Zz+Cz);。根据以上 4 个式子,可以求出,
3.从image变到perspective

4. 从perspective变到screen
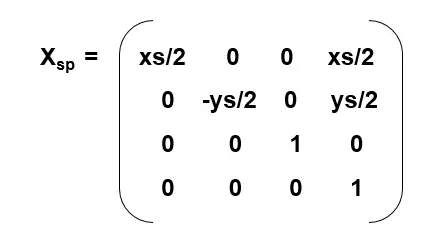

所以,一个3D物体显示到电脑屏幕上,要经过4重坐标系变换。 screen Xsp perspective (NDC) Xpi image Xiw world Xwm model
在实际的渲染引擎运行中,Xsp和Xpi基本不会变,因为你的屏幕分辨率很少会变动。Xiw会在相机移动和旋转时改变。Xwm会在物体平移,旋转,缩放时改变。
参考资料