除非你开发的游戏是一个纯经济模拟器,否则游戏中的角色基本都需要移动。在移动算法中,角色都会有一个当前的位置和可能附加的控制其移动的物理道具,比如一辆车,然后算法使用这些属性来计算出角色下一步应该在哪里。
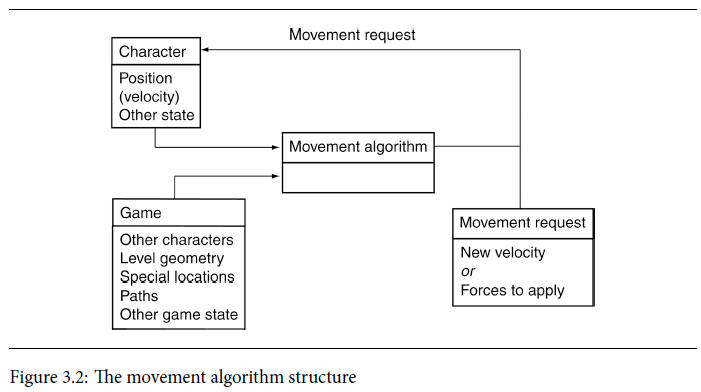
所有的运动算法都有相同的基本形式:它们获取关于自身状态和世界状态的几何数据,然后给出一个几何形式的输出,来表示它们接下来要进行的移动。下图显示了这一点,角色的速度属性设为可选项,因为只有特定的移动算法才需要它。
有些移动算法只需要很少的输入:例如,只需要角色的位置和要追赶的敌人的位置。另一些则需要与游戏状态和关卡几何结构进行大量的交互:例如,避免撞到墙壁的移动算法需要访问墙壁的几何图形来检查潜在的碰撞,比如开启《QQ飞车》手游里碰撞避免模式后赛车接近阻挡后会自动减速加拐弯。
输出也可以有所不同,在大多数游戏中,让移动算法输出所需的速度是常见操作,例如,一个角色可能会看到西边的敌人,并回应说它应该全速向西移动。而老游戏中的角色通常只有两种速度:静止速度和奔跑速度(可能还有步行速度,用于巡逻),所以这种游戏的移动系统输出只是一个移动的方向,这是运动学上的移动,它没有考虑角色的加速和减速。
现在考虑更多的物理性质是很普遍的,产生运动算法,我称之为 “转向行为”。这类型算法产生的移动不是运动学的,而是动态的。动态移动考虑了角色当前的运动,通常需要知道角色的当前速度以及它的位置,算法的输出是力或加速度,目的是改变角色的速度。
所以总的来说,动态性又增加了一层复杂性:假设你的角色需要从一个地方移动到另一个地方,运动学算法简单地给出了目标的方向,你的角色沿着那个方向移动,直到它到达,这时算法没有返回任何方向;而动态运动算法需要做的更多,首先,它需要向正确的方向加速,然后当它接近目标时,它需要向相反的方向加速,这样它的速度就会以正确的速度下降,从而在正确的位置减速。在本文和后面的所有文章中,我将所有动态运动算法都称作“转向行为”。
克雷格•雷诺兹(Craig Reynolds)发明了群集算法(flocking),该算法被用于无数电影和游戏中,使鸟群或其他动物的群体动起来。在后面的文章中,我们会讨论这个算法。因为 flocking 是最著名的转向行为,所以所有的转向算法有时被错误地称为 “flocking”。
一、二维运动
许多游戏都有在二维(2D)中工作的 AI,即使是在三维(3D)中渲染的游戏,通常也会有受到重力影响的角色,将他们粘在地板上并将他们的移动限制在二维空间。
许多运动 AI 可以在二维中实现,而大多数经典算法也只能在二维中实现。在研究算法本身之前,我们需要快速了解一下处理 2D 数学和运动所需的数据。
虽然一个角色通常由一个在游戏世界中占有一定空间的 3D 模型组成,但许多移动算法都假设角色可以被视为一个质点。碰撞检测、避障和其他一些算法使用角色的大小来影响它们的结果,但是移动本身假设角色是在一个点上。
这个过程类似于物理程序员将游戏中的物体视为位于质心的刚体,碰撞检测和其他力可以应用在物体的任何地方,但确定物体运动的算法将它们转换为只处理质心。
二、静态表示
二维角色有两个线性坐标表示对象的位置,这些坐标参考的坐标系是两个垂直于重力方向且彼此垂直的坐标轴,这组参考轴称为二维空间的标准正交基。
在大多数游戏中,几何图形通常以三维形式存储和呈现。模型的几何有一个三维标准正交基,包含三个轴:通常称为x、y 和 z。最常见的情况是 y 轴与重力方向相反;而 x 轴和 z 轴躺在地面平面上。游戏中的角色沿着用于渲染的 x 轴和 z 轴移动,如下图所示,由于这个原因,本章将使用 x 轴和 z 轴来表示二维的运动,尽管专门介绍二维几何的书籍倾向于使用 x 和 y 作为轴的名称。
任何角色都有一个朝向,朝向表示从参考轴开始的角度。在我们的例子中,我们使用一个逆时针弧度表示,从正 z 轴开始,这在游戏引擎中是标准设定;即在默认情况下,当方向为 0 时,角色将面向 z 轴的朝向。
有了位置(x, z)和朝向这三个值,就可以在游戏中给出角色的静态状态,如下图所示,
操作这些数据的算法或方程称为静态的,因为这些数据不包含关于角色移动的任何信息。我们能用如下数据结构表示该静态信息,
在本文及后续的文章中,我将使用 “orientation(方向)” 这个术语来表示一个角色所面对的方向。当角色时,我们将通过旋转矩阵来旋转它们使它们看起来是面向一个方向的,因此,一些开发人员将方向称为“rotation(旋转)”。在这一章里,我只用旋转来表示改变方向的过程,这是一个主动的过程。
一些涉及到 3D 几何的数学是复杂的,而三维中的线性运动非常简单,是二维运动的自然延伸,但是表示一个方向可能会产生一些棘手的结果。作为一种折衷方案,开发人员通常使用 2D 和 3D 计算的混合,也就是众所周知的 2.5D 计算,或者有时被称为四自由度计算。
在 2.5D 空间中,我们处理一个完整的三维位置,但是将方向表示为一个单一的值,就像我们在 2D 空间中一样。当你考虑到大多数游戏中的角色都受到重力的影响时,这是非常合理的。大多数时候,角色的三维空间会因为被拉到地上而受到限制,尽管跳跃、从壁架上跌落和使用电梯都需要在三维空间中移动,它实际上主要还是在二维空间中运行的。即使上下移动,角色通常也保持直立,在行走或跑步时,可能会有轻微的向前倾斜,或者从墙上向外倾斜,但这种倾斜并不影响角色的移动,它主要是一种动画效果。如果一个角色保持直立,那么我们唯一需要考虑的是它的旋转方向。这正是我们在处理 2.5D 时所利用的情况,在大多数情况下,为了获得数学上的简化是值得减少灵活性的。
当然,如果你在写一个飞行模拟器或太空射击,那么所有的方向对 AI 来说都是非常重要的,所以你必须支持三维方向的数学运算。另一方面,如果你的游戏世界是完全平坦的,角色不能以任何其他方式跳跃或垂直移动,那么就需要一个严格的 2D 模型。在绝大多数情况下,2.5D 是最佳解决方案。我将在后面的几篇关于移动系统的文章中最后一篇介绍全 3D 运动,但除此之外,本章中描述的所有算法都是设计用于 2.5D 的。
三、动力学
每个角色都有两个相关的信息:它的位置和方向。我们可以仅基于位置和方向创建运动算法来计算目标速度,并根据输出速度立即作出改变。虽然这理论上可行的,但它会使得游戏不太真实。
牛顿运动定律的一个结果是速度在现实世界中不能瞬间改变,如果一个角色正在向一个方向移动,然后立即改变方向或速度,它可能看起来很奇怪,为了使动作平滑,或者为了处理不能快速加速的角色,我们需要使用某种平滑算法或者考虑当前的速度并使用加速来改变它。为了支持这一点,角色保持它当前的速度和位置,算法可以在每一帧稍微改变速度,给出一个平滑的运动。
角色需要同时记录他们的线速度和角速度:线速度有 x 分量和 z 分量,这是角色的速度表示的标准正交基。如果我们在 2.5 维空间中工作,那么就会有 x y z 三个线速度分量;角速度代表了角色的方向变化的速度,这是由一个单一的值给出的:方向改变的每秒弧度数。
我把角速度称为旋转,而线速度通常简称为速度。因此,我们可以将一个角色的所有运动数据表示成如下的数据结构结构:
转向行为操作着上述运动学数据,它会返回加速度来改变角色的速度,以便在关卡中移动他们,输出形式可以表示如下:
3.1 独立朝向
注意,角色移动的方向和它面向的方向是不存在绝对绑定的:角色可以朝向 x 轴方向,却是沿着 z 轴移动。但一般情况下,大多数游戏角色不这样做,他们会调整自己的方向来使得朝着他们面向的方向移动。
许多转向行为完全忽略了朝向,它们直接对角色数据的线性部分进行操作,在这些情况下,应该更新方向,使其与运动方向相匹配。这可以通过直接将方向设置为运动方向来实现,但是这样做可能意味着方向会突然改变。
一个更好的解决方案是朝期望的方向移动它的一个比例的方式,将旋转平滑分布在多个帧。在下图中,角色在每一帧中都将其方向改变为当前运动方向的一半,
其中,三角形表示方向,灰色阴影表示角色在前一帧中的位置。
3.2 更新位置和朝向
物理引擎可以用来更新角色的位置和方向,一般情况下,即使游戏使用了物理引擎,开发人员通常也更偏好只使用它的碰撞检测,然后写自定义的移动控制器。所以如果你需要手动更新位置和方向,你可以使用如下的一个简单算法:
这些更新使用了高中物理运动方程。如果帧速率很高,那么传递给这个函数的更新时间可能非常小,这个时间的平方可能更小,因此加速度对位置和方向的贡献将很小,什么必要。更常见的做法是使用简单的“牛顿-欧拉-1(Newton-Euler-1)”积分方法进行更新,
这是游戏中最常见的更新。注意,在这两个代码块中,我都假设我们可以对向量进行常规的数学操作,比如加和乘一个标量。根据所使用的语言,可能需要用函数调用替换这些基本操作。
3.3 可变帧速率
在本文中,假设速度的单位都是每秒,而不是每帧;以前的游戏通常使用帧速度,但这种做法基本上已经消失了;当然,有一种情况例外,就是游戏在一个单独的执行线程中以固定的帧速度进行处理,独立于图形更新,例如Unity的FixedUpdate函数相对于它的可变更新。但即使有固定帧间隔的函数,支持可变的帧速率还是更加灵活,所以一般还是用时间作为速度的衡量单位。
举个例子,如果已知字符以每秒 1 米的速度移动,而最后一帧的持续时间是 20 毫秒,那么他们需要移动 20 毫米。
3.4 力和驱动
在现实世界中,我们通常是施加一个力,而不是简单地一个加速度来让物体移动。这个施加的力引起物体动能的变化,从而使物体会加速,但加速度取决于物体的质量,当力一定时,质量越大,加速度就越小。
这是物理引擎使用的方法:AI 通过施加力来控制角色的运动,这些力代表了角色影响其运动的方式,尽管这种方法在人类角色中并不常见;但在驾驶游戏中,这种方法在控制汽车方面几乎是普遍的:引擎的驱动力和与方向盘相关的力是 AI 控制汽车运动的唯一方式。
因为大多数完善的转向算法输出的是加速度,而很少直接使用力。通常,运动控制器通过加速度计算角色的力的过程称为 “驱动(actuation)”。驱动以所需的速度变化作为输入,这种变化可以直接应用于运动学系统,然后驱动器计算可以应用的力的组合,以尽可能接近所需的速度变化。在最简单的层面上,通过加速度乘以质量就得到了力,这是假设角色能够施加任何力,然而这并不绝对,例如,静止的汽车不能侧向加速。驱动是 AI 和物理集成中的一个主要主题,在后续的文章我们还将继续谈及到。
总之一句话,转向算法输出加速度,加速度转变成力,力借助物理引擎来控制角色运动。