本文描述的转向行为概念是在前一节运动学算法的基础上扩展增加了速度和旋转,在某些类型中,比如驾驶游戏,转向行为占主导地位;在其他类型的游戏中,它们更依赖于具体游戏内容:有些角色可能需要它们,有些角色则不需要。
现有的各种转向行为算法,命名往往含糊不清或互相冲突。随着这一领域的发展,还没有出现明确的命名方案来区分单个原子转向行为和将多个原子转向行为结合在一起的复合行为。在这本文中,我将区分这两种行为:基本行为和由基本行为组成的复合行为。
虽然在各种论文和代码样本中有大量的转向行为命名,但其中大多是一个或两个主题的变种,我们不打算把所有的行为都分类,也很难做到涵盖所有行为。取而代之,我会先提取出这些行为算法的基本通用结构,然后再看一些具有不寻常特征的特例。
一、转向基础
总的来说,大多数转向行为具有类似的结构:以正在运动的角色的运动学状态和有限数量的目标信息作为输入。其中,目标信息取决于具体应用,比如对于追逐或逃避行为,目标通常是另一个移动的角色;再比如避障行为时的寻路算法,目标就是指定路径。
转向行为的输入集并不总是以对 AI 友好的格式提供,比如,避障行为需要获取关卡的障碍信息,这可能是一个昂贵的过程:使用射线检测或试着在关卡中移动来检查角色预期的移动。
还有许多转向行为是对一组目标进行操作。例如,著名的群体行为(flocking behavior)算法中涉及到向群体的平均位置移动,这可能涉及到对整个集合的属性进行平均,例如,寻找它们的质心;或者可能涉及到对它们进行排序或搜索,例如远离最近的捕食者或避免撞上其他在碰撞轨道上的角色。
注意,转向行为并不是试图做所有的事情。在追逐一个角色时,没有躲避障碍的行为。每个算法只做一件事,只接受所需的输入。为了得到更复杂的行为,我们需要使用算法来组成多个转向行为,并使它们一起运作。
二、变量匹配
最简单的转向行为试图匹配字符的一个或多个元素的运动学单一目标运动学。
例如,我们可能会尝试匹配目标的位置,而不考虑其他元素。这包括向目标位置加速和在接近目标位置时减速。或者,我们可以尝试匹配目标的方向,旋转以便与它对齐。我们甚至可以尝试匹配目标的速度,沿着平行的路径跟踪它,复制它的运动,但保持固定的距离。
可以创建一个通用的转向行为来匹配变量的任何子集,并简单地告诉它要匹配哪个元素组合,但这并不是特别有用。我自己也犯了这个错误。当运动学的多个元素同时匹配时,问题就出现了,他们很容易发生冲突。我们可以独立匹配目标的位置和方向,但是位置和速度呢?如果我们在匹配速度,那么我们就无法做到同时接近它。
一种更好的技术是为每个元素使用单独的匹配算法,然后在以后将它们组合到正确的组合中。这允许我们使用本章中的任何转向行为组合技术,而不是硬编码。设计转向行为结合算法是解决冲突的理想方法。
对于每一个匹配的转向行为,都有一个相反的行为试图尽可能远离匹配。试图捕捉目标的行为与试图躲避目标的行为正好相反;一种试图避免撞到墙壁的行为,与之相反的是拥抱墙壁的行为(可能用于扮演胆小的老鼠),等等。正如我们在运动学寻找行为中看到的,相反的形式通常是对基本行为的简单调整,我们将一对互为相反的转向行为放在一起考虑,而不是把他们分开成单独的部分。
三、追逐和逃跑
“追逐” 试图匹配角色和目标的位置。就像运动学搜索算法一样,它找到目标的方向并尽可能快地朝目标前进。因为转向输出现在是一个加速,它将加速尽可能多。
显然,如果它继续加速,它的速度会越来越大。大多数角色都有他们可以运动的最大速度;它们不能无限地加速。最大值可以是显式的,记录在一个变量或常数中,或者它可能是与速度有关的阻力的函数,速度越快,角色加速度就越小直到 0。
有了明确的最大速度,就会定期检查角色的当前速度(速度向量的长度),如果超过最大速度,就会进行调整。这通常是更新函数的后处理步骤。它通常不是在转向行为中执行的。
依赖于物理引擎的游戏通常包括拖动而不是最大速度(尽管它们可能使用最大速度也为了安全)。没有最大速度,更新不需要检查和修改当前的速度,拖动(应用在物理更新功能)自动限制最高速度。
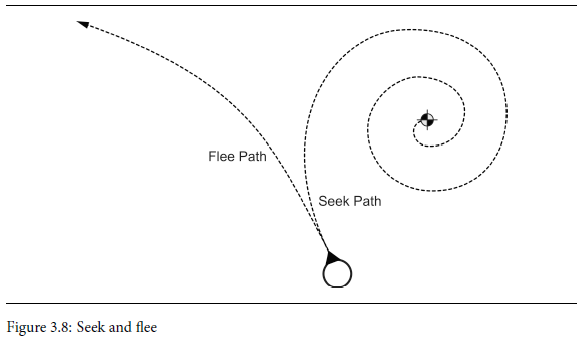
拖动还有助于解决该算法的另一个问题。因为加速度总是指向目标,如果目标在移动,寻找行为将会结束在轨道上而不是直接朝它移动。如果系统中存在阻力,那么轨道就会变成一个向内的螺旋。如果拖拽足够大,玩家将不会注意到螺旋,而会看到角色直接移动到目标。
上图说明了从寻求行为和它的对立面,逃离的路径。
3.1 伪代码
动态追逐的实现和运动学算法版本很相近,
注意,我删除了运动学版本中包含的方向变化。我们可以像以前那样简单地设置方向,但是更灵活的方法是使用可变匹配使字符的脸朝着正确的方向。下面描述的对齐行为为我们提供了使用角加速度改变方向的工具。“看着你正在去的地方”的行为使用这个面向移动的方向。
3.2 性能
时间和空间复杂度仍都是 O(1)。
3.3 逃跑
逃跑是寻求的反义词。它会尽可能地远离目标。就像运动学逃逸,我们只需要翻转函数的第二行项的顺序
角色将会在与目标相反的方向上移动,尽可能快的加速。
四、到达
“追逐” 总是会以最大的可能加速向它的目标前进。如果目标一直在移动,角色需要全速追赶,这是对的。当角色到达目标时,它会越过、反转并振荡穿过目标,或者它更有可能绕着目标轨道运行而没有靠近目标。
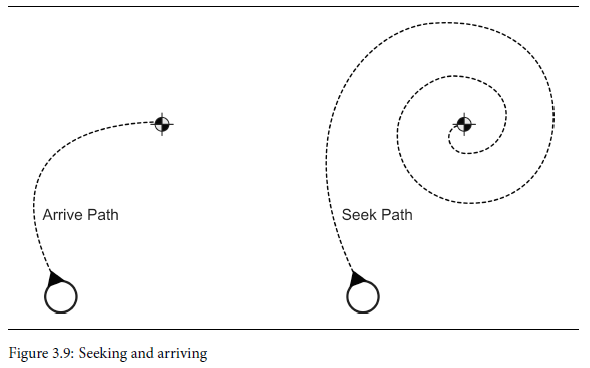
如果角色应该到达目标,它需要减速以便它精确地到达正确的位置,就像我们在运动学到达算法中看到的那样。上图显示了每个固定目标的行为。虚线显示了 “到达” 和 “寻找” 的路径。“到达” 直接去到它的目标,而 “寻找” 处于一段振荡状态,在动态寻道中,振荡并不像在运动学寻道中那样糟糕:角色不能立即改变方向,所以它看起来是摆动而不是在目标周围晃动。
“动态到达”行为比运动学版本复杂一点。它使用了两个半径。到达半径,即可接受误差半径,这一部分跟运动学版本一样,当角色足够接近目标就停止运动了,避免微小误差导致无法及时停止。第二个半径要大得多,进入的角色将开始减速当它通过这个半径。算法为角色计算一个理想的速度。在减速半径边界上,速度等于它的最大速度;而在目标点,它是零(我们希望到达时速度为零);在这两者之间,期望的速度是一个内插的中间值,由与目标的距离控制。
与前面一样计算目标的方向,然后结合所需的速度给出目标速度。该算法依据角色的当前速度向量,计算出将其转换为目标速度向量所需的加速度。然而,我们不能立即改变速度,需要算出加速度,加速度的值是根据在固定的时间尺度内达到目标速度来计算的。这和“运动学到达”的过程是完全一样的,在“运动学到达”中我们试图使角色在四分之一秒内到达目标。在这里,由于有一个额外的间接层(加速度通过影响速度间接地影响位置),动态到达的固定时间周期通常会小一些,我们将使用 0.1秒 作为一个好的参考值。
4.1 伪代码
完整的算法大致如下,
4.2 性能
时间和空间复杂度仍都是 O(1)。
4.3 实现注意事项
许多实现不使用可接受误差半径,因为角色会减速到达它的目标,没有振荡的可能性,所以移除目标半径通常没有明显的区别。然而,在低帧率或角色具有较高的最高速度和低加速的情况下,它可能是重要的。一般来说,在任何目标周围设置一个误差范围是一种很好的做法,以避免令人讨厌的不稳定性。
4.4 离开
如果我们需要离开一个目标,我们不太可能想要先以极小的加速度(可能为零)加速,然后再增加,我们更可能加速越快越好。