机器学习 · 总览篇 XI - 蔡康的博客

总览篇第4篇到第10篇主要是围绕着模型来介绍的，具体讲述的是机器学习模型的构建和学习的过程；本文是总览篇的最后一篇文章，介绍特征工程，准确来说特征工程是独立与机器学习存在的一个主题，但却是机器学习应用中不可缺少的一环。特征工程在2006年深度学习大热之前，是与“模型”处于同等地位的内容，随着深度学习的兴起，特征工程一部分工作由深度学习的深度网络完成，使特征工程的地位明显降低，然而特征工程真的就因此不重要了吗？并不是，特征工程在当今时代仍然发挥着重要的作用，甚至可以说是无处不在。

文章首发于我的博客，转载请保留链接 ;)

一、特征工程是什么

特征工程是一个过程，一个“利用数据相关领域知识来创造让机器学习算法能运作的特征”的过程。特征工程虽然是一个非正式的主题，通常情况下也并没有被列入到机器学习必要的元素中，但在机器学习实际应用中确实是不可缺少的元素。从这个角度看，有点类似于“空气之于人”，平时不重视，但十分重要，并且无处不在。

首先，特征是什么？特征是做分析或预测的所有独立样本共享的一种属性，所有对模型有影响的属性都能成为特征，除了属性意义之外，特征的目的是让模型更容易挖掘问题的语义，从而帮助模型解决问题。

然后，特征工程就是一大箩筐围绕着特征要做的事情的集合，以服务于后面模型的学习。特征工程与机器学习关系的示意图如图1所示，

图1 特征工程与机器学习

从图1可以看到，特征工程与机器学习有交叉的地方，但更多是扮演着独立的预处理过程的角色。特征工程的大致流程包括：

特征构建
特征清洗
检查特征如何与模型一起使用
特征改进。常见的包括单维特征处理、特征降维。
重复1-4步，直到工作完成。

文本重点介绍内容：第二节介绍第1步的特征构建，第三节介绍第2步的特征清洗，第四节介绍第4步中的单维特征处理，第五节介绍第4步中的特征降维。本文内容较多且杂，因为特征工程的工作本身就多且杂。

二、特征构建

通常有这么一种认知，认为机器学习会彻底占领人类专家擅长的领域，其实并不然，至少现阶段是错误的。特征构建作为机器学习流程的第一步（如图2所示），也是很重要的一步，是十分依赖专家知识的。

图2 特征构建

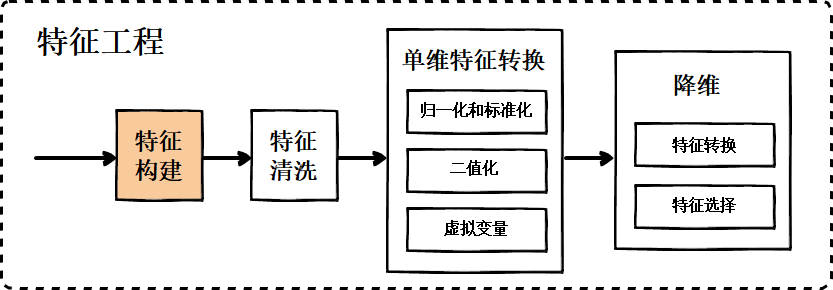
特征构建是指从原始数据中人工的找出一些对模型学习有用的具有物理意义的特征。 需要花时间去观察原始数据，思考问题的潜在影响因素。为了构建特征，我们应该需要做到以下两点：

培养对领域的认知、数据的敏感性、机器学习实战经验，这些能有效地帮助我们进行特征构建，但都需要一定的积累和沉淀。
除此之外，特征构建还有一些即时可以使用的技巧，数据的分割和结合：分割是指将某一种数据细化成多种数据，提供更多的信息，提高模型准确率；而结合是相反的过程，将冗余表达的信息合并在一起，提高模型收敛效率，典型有对于逻辑回归等广义线性模型，组合特征方法是一个十分常用并且有效的特征构建方法，比如将特征A [1, 0, 1]与特征B [0, 1] 组合，通过特征向量的叉乘构成新的组合特征C [0, 0, 0, 1, 0, 1]。

为了方便理解，以下给出两个关于属性分割和结合的实际例子，

【场景1-属性分割】根据大学生前两个学期的表现来预测他是否能在大学毕业时获得优秀毕业生的称号。【分析】直观的当然应该将学习成绩作为一个特征属性，但进一步进行考虑，通常专业必修课课成绩对评选影响更大，而非专业选修课影响会比较小，学习成绩又是本任务一个十分重要的影响因素，所以分开更合理，那么这种情况就是按学科将学习成绩属性分割。

【场景2-属性结合】预测大学生毕业后的薪资水平【分析】对于该任务，影响因素大概有学校、专业、学习成绩、获奖情况、课程项目经历、公司实习经历等，在这种情况下影响因素本身就较多，而且都相对比较重要。我们已有的数据包含了学生各科的成绩，如果直接拿来作为特征，根据《总览篇 VII 三要素之策略-正则化》可知，特征过多可能会导致过拟合；而过多太细化的特征实际影响并不大。所以，跟属性分割相反，将所有成绩做平均，或者最多将部分课程成绩结合分成专业课成绩和非专业课成绩是更合适的做法。

可以看到，特征的构建是一个精准权衡的过程，需要做到信息 “不冗余的完整”，是个非常麻烦的问题，书里面也很少提到具体的方法，需要对问题有比较深入的理解。

三、特征清洗

也叫数据清洗，它是特征工程的第二步：它是发现并纠正数据文件中可识别的错误的最后一道程序，包括检查数据一致性，处理无效值和缺失值等；为了解决数据不平衡带来的学习无效的问题，还需要做到数据相对均衡。

图3 特征清洗

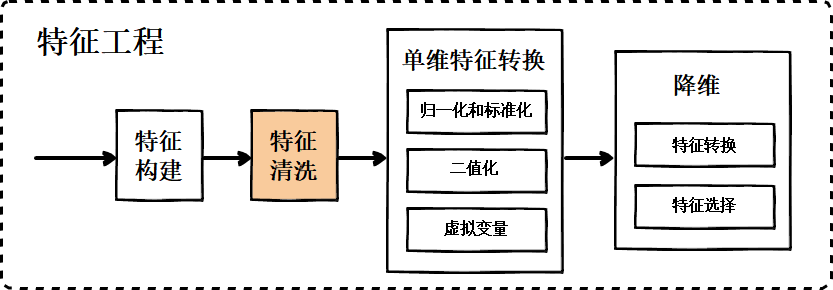
4.1 无效值和缺失值的处理

由于一些因素，数据中可能存在一些无效值和缺失值，需要给予适当的处理。常用的处理方法包括：

1. 估算（Estimation）。 使用缺失数值所在行或列的均值、中位数、众数、最值等来替代缺失值。或者根据样本其它有相关性的数据来估算缺失数据。 2. 样本删除（Casewise Deletion）。 当受到影响的样本占总样本比例较低，或者受影响的特征维度十分重要时，将有问题的样本删除是一种对学习效果影响较小的做法。 3. 变量删除（Variable Deletion）。 当受到影响的样本较多，或者受影响的特征维度不太重要时，将有问题的样本删除是一种对学习效果影响较小的做法。有同学会说受影响的样本较多，受影响的特征维度又很重要怎么办？这个时候如果能重新收集数据最好，实在不行就需要在以上三种处理方法中权衡选择了。

【场景3-无效值和缺失值的处理】根据人的体检指标对疾病自动进行诊断【分析】如果医院数据库的误操作将某一列全部删掉，或者某一位护士负责的那部分体检人的某列数据全部删掉。当缺失值是右眼视力，由于通常人两眼视力是接近的，所以可以用估算的方法，比如直接将左眼视力拷贝到右眼视力；当缺失值是少数体检人的部分重要数据，可以将样本剔除，再进行训练；当缺失值是身高，身高对疾病诊断的重要性不高，所以可以用变量删除的方法，将身高这一维度去除

采用不同的处理方法可能对分析结果产生影响，尤其是当缺失值的出现并非随机且变量之间明显相关时。因此，在数据收集中应当尽量避免出现无效值和缺失值，保证数据的完整性。

4.2 采样

4.2.1 样本均衡

在分类中，训练数据不均衡是指不同类别下的样本数目相差巨大。比如对于一个二分类任务，如果训练集中类别1的样本数与类别2的样本数比值为100:1，使用逻辑回归进行分类，那么其结果很可能将所有样本都分类为类别1。样本不均衡会导致训练出的逻辑回归模型无效的原因在于，逻辑回归模型的代价函数是基于最大似然估计（MLE）的，某一类别的样本如果占绝大多数，会导致代价函数基本没有参考意义，因为模型当然会着重保证该类样本分类正确。

实际应用中，训练样本数据不均衡是常见并且合理的，比如在欺诈交易识别中，绝大部分交易是正常的，只有极少部分的交易属于欺诈交易；敏感头像（政治敏感、黄色相关的头像）检测中，绝大部分头像是正常的，只有极少部分头像属于政治敏感、黄色相关的。

通常有如下样本均衡方法：

最直接的方法就是扩充数据集，去收集更多的少样本类别的样本；
然后就是拷贝过采样（over-sampling），即对少样本类别进行拷贝过采样来增加类别的样本量，以达到类别间样本均衡。
欠采样（under-sampling），即对多样本类别进行欠采样来减少类别的样本量，以达到类别间样本均衡。
人造数据，与拷贝过采样直接拷贝副本的方法不同，这里指的是构造全新样本的方法，代表性方法是SMOTE法，JAIR期刊2002年的文章《SMOTE: Synthetic Minority Over-sampling Technique》提出了一种过采样算法SMOTE，概括来说，本算法基于“插值”来为少数类合成新的样本。
除此之外，对于boosting算法，它是采用多个弱学习器组合形成的强学习器，所以可以在进行弱学习器训练时随机选取等量类别的样本，当然，每个弱学习器都重新选择新的样本。

4.2.2 样本权重

为了解决不同类别样本量差别过大的问题，样本均衡方法是从处理样本本身出发的，样本权重方法是从改变分类算法来实现的，在代价函数中增加少样本类别的样本权值，降低多样本类别的样本权值，其实这种做法等价于过采样和欠采样方法。

四、单维特征处理

单维特征处理指的不仅仅是对单个特征的处理，也包含对多特征中的某一维特征的处理。

图4 单位特征处理

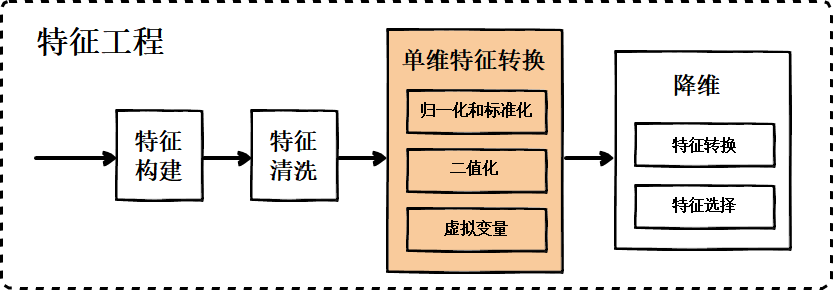
4.1 归一化（Normalization）和标准化（Standardization）

归一化和标准化主要是为了应对“特征不同维度的量级可能差别过大而导致的问题”，比如对于一个两个维度量级差别很大的特征，在模型训练阶段对目标函数进行梯度下降时，在未归一化和归一化这两种情形下梯度过程可如图5所示，

图5 单位特征处理

从图5中可以看到，相比于未归一化，数据归一化后最优解的寻优过程明显会变得平缓，就更容易正确地收敛到最优解。归一化和标准化这两个概念由于长期的混用，到现在通常指的是同一个概念 —— 无量纲化。但究归一化和标准化差别的话，归一化内容稍微广泛一些，通常包含线性归一化，比如

$x'=\frac{x-min(x)}{max(x)-min(x)}$

还包含非线性归一化，比如 log(x)、exp(x)、tanh(x)。

而通常意义上的标准化指代比较狭隘，指的是根据均值和标准差实现的线性放缩，如下所示，

$x'=\frac{x-\mu }{\sigma }$

【场景-归一化】根据房屋面积和卧室数量对房屋售价的预测任务【分析】虽然在同一个地段接近年份的房子，房屋售价通常是受房屋面积影响，但卧室数量也有一定的影响。但房屋面积通常是几十甚至数百平米，而卧室数量通常是个位数，如果直接将该样本送入训练，则代价函数的轮廓会是以房屋面积值为长轴的扁长形状，在找最优解时，梯度下降的过程不仅曲折，而且非常耗时。这个时候如果对房屋面积和卧室数量分别做线性归一化或标准化，能明显提高最优化过程的效率。

4.2 二值化（定量特征离散化）

对于某些应用场景，我们更在乎是与否，而不关注程度，这种时候将定量特征的连续值转换成01值能提高学习效率，这种方法称之为二值化。定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0（相反也可），公式表达如下，

$x'=\left\{\begin{matrix} 1, \ x>threshold\\ 0,\ x\leq threshold \end{matrix}\right.$

如下是二值化应用的一个场景，

【场景-二值化】对于一个根据学生成绩来对表现进行分类的分类任务【分析】假如我们在音乐学习成绩这一项上通常只关心“及格”还是“不及格”，那么需要将定量的考分，转成“1”和“0”，分别表示及格和不及格，及格阈值是60分，那么分数大于等于60则转换成特征1，分数小于60则转换成特征0

4.3 虚拟变量（定性特征编码化）

虚拟变量，也叫哑变量、离散特征编码，可用来表示分类变量、非数据因素可能产生的影响。虚拟变量可划分成两种数据类型：

1. 离散特征的取值之间有大小的意义。例如：尺寸（L、XL、XXL）。这种情境很简单，直接用1，2，3来表示是合理的。 2. 离散特征的取值之间没有大小的意义。例如：颜色（Red、Blue、Green）。这种情况下，直接用1，2，3来表示存在一定的问题，因为模型的本质是函数，用1，2，3蕴含了额外的大小信息，比如2是在1和3之间，而实际上我们并不期望蓝色是介于红色和绿色之间，所以这样表示是不合理的。这个时候就需要借助热编码（one-hot encoding）。下图是《决战！平安京》对式神阵容进行热编码表征的示意图，

图6 热编码特征

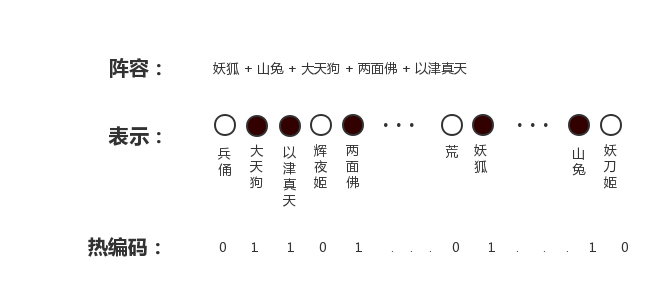
如下是虚拟变量应用的一个场景，

【场景-虚拟编码】对于一种MOBA类游戏，我们要根据游戏世界状态进行游戏AI的操作训练【分析】英雄的BUFF类型和层数是影响操作的因素之一，比如《决战！平安京》中荒叠满5层星月之力就可以放出最大伤害的大招，那么在这个情境中，BUFF不同类型之间没有大小的意义，所以应采用类似于上图式神阵容那样的热编码形式表示；而BUFF不同层数之间有大小差别，所以可以直接用对应数字进行表示。

五、降维

在实际操作时如果发现过拟合问题，除了考虑增加训练样本数，我们还应该考虑特征维度是否可以减少。有个东西叫curse of dimensionality，维度越高，数据在每个特征维度上的分布就越稀疏，要达到同样的效果需要的数据量呈指数级增长，这对机器学习算法基本都是灾难性的。

有人会说，特征数量过多，做前面的特征构建阶段砍掉不就行了。而事实上，很多问题的特征就是砍不掉。比如要研究某个罕见病跟什么基因有关，人类已知的基因有几千个，但是每个基因的真正作用目前技术并不能完全了解，能直接排除掉吗？并不能，这个时候就需要借助降维手段。事实上，在实际应用场景中如果特征维度过高，采用降维手段，包括特征转换、特征选择，很有可能提高学习效果。

图7 降维

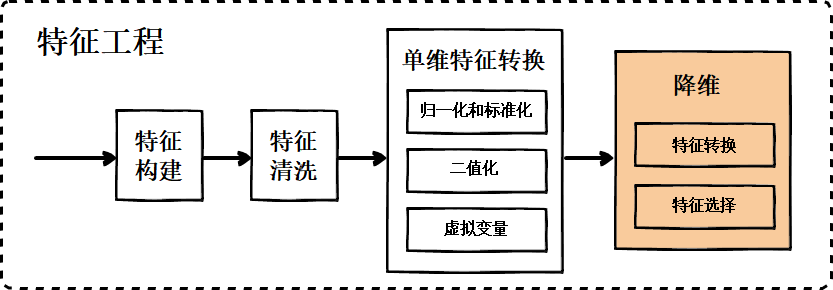
5.1 特征转换

主成分分析（Principal Component Analysis，PCA）和线性判别分析（Linear Discriminant Analysis，LDA）是最常见和有效的特征转换降维方法，随着深度学习的兴起，使用深度学习的手段进行降维也十分有效。

PCA

相比于LDA，PCA还更常用一些，PCA优势在于它采用无监督（unsupervised）方式，不要求样本带类别信息，PCA的无监督优势很吸引人，因为自然界中任何信息都属于无类别信息，只有被人定义了类别的信息才是带类别信息，所以带类别信息相对于全体信息来说是十分稀有的。由于任何多维特征都可以使用PCA处理，所以PCA更像是一个通用的预处理方法；PCA的主要作用是挖掘主成分和降维；PCA的本质思想是使主成分或者说降维后的特征每个维度之间方差最大，熵，其物理意义是体系混乱程度的度量，所以也可以说PCA是使熵尽可能大。以下是PCA的推导过程

去除均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值排序
保留前N大的特征值对应的特征向量作为新空间的基向量
将数据转换到上面得到的N个特征向量构建的新空间中（实现了特征压缩）

上 PCA 的 python 代码，需且仅需 numpy支持，

# coding=utf-8

from numpy import *

def pca(dataMat, topNfeat=1):
    """
    pca特征维度压缩函数
    :param dataMat: 数据集矩阵
    :param topNfeat: 需要保留的特征维度，即要压缩成的维度数
    :return:
    """
    #求数据矩阵每一列的均值
    meanVals = mean(dataMat, axis=0)
    #数据矩阵每一列特征减去该列的特征均值
    meanRemoved = dataMat - meanVals
    #计算协方差矩阵，除数n-1是为了得到协方差的无偏估计
    covMat = cov(meanRemoved, rowvar=0)
    #计算协方差矩阵的特征值eigVals及对应的特征向量eigVects
    eigVals, eigVects = linalg.eig(mat(covMat))
    #argsort():对特征值矩阵进行由小到大排序，返回对应排序后的索引
    eigValInd = argsort(eigVals)
    #从排序后的矩阵最后一个开始自下而上选取最大的N个特征值，返回其对应的索引
    eigValInd = eigValInd[:-(topNfeat+1):-1]
    #将特征值最大的N个特征值对应索引的特征向量提取出来，组成压缩矩阵
    redEigVects = eigVects[:,eigValInd]
    #将去除均值后的数据矩阵*压缩矩阵，转换到新的空间，使维度降低为N
    lowDDataMat = meanRemoved * redEigVects
    #利用降维后的矩阵反构出原数据矩阵(用作测试，可跟未压缩的原矩阵比对)
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    #返回压缩后的数据矩阵即该矩阵反构出原始数据矩阵
    return lowDDataMat, reconMat

if __name__ == '__main__':
    data = [[1,0],[3,2],[2,2],[0,2],[1,3]]
    lowDData, recon = pca(data)
    print(lowDData)
    print(recon)

LDA

相比于PCA，LDA依赖类别信息，所以LDA没有PCA使用的那么广泛，但在有类别信息的情况下，LDA还可以作为一个独立的判别算法存在，给定了训练数据后，将会得到一系列的判别函数（discriminate function），之后对于新的输入，就可以进行预测了。PCA是希望样本投影的方差尽可能大，而LDA是希望同类别样本投影尽可能靠近而不同类别样本投影尽可能远离，LDA的这种思想也许用公式更能体现，下面是两类别LDA的目标函数，

$\underbrace{arg\;max}_w\;\;J(w) = \frac{||w^T\mu_0-w^T\mu_1||_2^2}{w^T\Sigma_0w+w^T\Sigma_1w} = \frac{w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw}{w^T(\Sigma_0+\Sigma_1)w}$

其中分子就是两个类别的中心距离，分母两类同类别样本方差（协方差）之和，要让分子尽可能大，分母尽可能小。

上 PCA 的 python 代码，需且仅需 numpy支持，

# coding=utf-8

from numpy import *

def lda(c1, c2, topNfeat=1):
    """
    lda特征维度压缩函数
    :param c1: 第一类样本矩阵，每行是一个样本
    :param c2: 第二类样本矩阵，每行是一个样本
    :param topNfeat: 需要保留的特征维度，即要压缩成的维度数
    :return:
    """
    # 第一类样本均值
    m1 = mean(c1, axis=0)
    # 第二类样本均值
    m2 = mean(c2, axis=0)
    # 所有样本矩阵
    c = vstack((c1, c2))
    # 所有样本的均值
    m = mean(c, axis=0)
    # 第一类样本数
    n1 = c1.shape[0]
    # 第二类样本数
    n2 = c2.shape[0]
    # 求第一类样本的散列矩阵s1
    s1=0
    for i in range(0,n1):
        s1 += (c1[i,:]-m1).T*(c1[i,:]-m1)
    # 求第二类样本的散列矩阵 s2
    s2=0
    for i in range(0,n2):
        s2 += (c2[i,:]-m2).T*(c2[i,:]-m2)
    # 计算类内离散度矩阵Sw
    Sw = (n1*s1+n2*s2)/(n1+n2)
    # 计算类间离散度矩阵Sb
    Sb = (n1*(m-m1).T*(m-m1) + n2*(m-m2).T*(m-m2))/(n1+n2)
    # 求最大特征值对应的特征值和特征向量（重点）
    eigvalue, eigvector = linalg.eig(mat(Sw).I*Sb)
    # 对eigvalue从大到小排序，返回对应排序后的索引
    indexVec = argsort(-eigvalue)
    # 取出最大的特征值对应的索引
    nLargestIndex = indexVec[:topNfeat]
    # 取出最大的特征值对应的特征向量
    W = eigvector[:,nLargestIndex]
    # 返回降维后结果
    return W

if __name__ == '__main__':
    data1 = [[1, 0], [3, 2]]
    data2 = [[0, 1], [1, 3]]
    w = lda(array(data1), array(data2), 2)
    print(w)

PCA和LDA的比较

相同点：

两者的作用是用来降维的
两者都假设符合高斯分布

不同点

LDA是有监督的降维方法，PCA是无监督的。
LDA降维最多降到类别数K-1的维数，PCA没有这个限制。
PCA追求的是在降维之后能够最大化保持数据的内在信息，并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据的区分作用并不大，反而可能使得数据点揉杂在一起无法区分。这也是PCA存在的最大一个问题，这导致使用PCA在很多情况下的分类效果并不好。具体可以看下图8，

图8 PCA 和 LDA 的分类效果比较

图8是使用 PCA 和 LDA 分别降维后重构回原维度空间的示意图，从两图对比可以看到，若使用 PCA 将数据点投影至一维空间上时，左边 PCA 使得原本分类的样本更难分类了，右边 LDA 更有助于分类。

深度学习

用深度学习的方法降维的结果表示的物理意义就没那么直观，但到目前来看已经成为最热门也最有效的降维方法。与 PCA 和 LDA 分别对应，深度学习降维方法也可以分为无监督和有监督两大类：

1. 无监督深度学习降维方法。让深度学习大热起来的那篇 Hinton 2006的文章，在分层预训练阶段，每一层都被看作一个玻尔兹曼机（Restricted Boltzmann Machine，RBM），并用统计概率上的马尔科夫随机场（Markov Random Fields）来解释，由多层 RBM 堆叠而成的网络被称为深度置信网络（Deep Belief Network，DBN）。RBM 组成的 DBN 是一种无监督的降维方法。另一种同样大热无监督深度学习降维方法是堆叠自编码器（stack auto-encoder，SAE），SAE 就是一种尽可能复现输入信号的神经网络；

2. 有监督深度学习降维方法。常见的有监督深度神经网络大类包括多层感知机（Multiple-Layer Perception，MLP），卷积神经网络（Convolutional Neural Network，CNN），循环神经网络（Recurrent Neural Network，RNN）及其变种，各种深度神经网络的抽出某一层中间表示作为特征，都可以当做是降维后的特征。以 CNN 为例，每一个节点都是一个卷积过滤器，训练获得的系数就是每个过滤器的参数。

5.2 特征选择

分为：过滤法（Filter）、封装法（Wrapper）以及嵌入法（Embedded）。

5.2.1 过滤法（Filter）

过滤是一种相对比较简单粗暴的方法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。

移除低方差的特征 (Removing features with low variance)。与 PCA 降维方法相比，这种方法也是从方差的角度出发，不过更加简单暴力，直接将方差低的特征维度直接移除。
单变量特征选择 (Univariate feature selection)。单变量特征选择的原理是分别单独计算每个特征（自变量）对标签（因变量）的某个统计指标，根据该指标来判断哪些指标重要，剔除那些不重要的指标。其中对于分类问题（即标签 y 离散），统计指标通常是卡方(Chi2)检验；对于回归问题（即标签 y 连续），统计指标通常是 Pearson 相关系数 (Pearson Correlation)。

5.2.2 包装法（Wrapper）

包装法，每次根据某种规则标准，选择若干特征，或者排除若干特征。

典型的方法是递归特征消除（Recursive Feature Elimination，EFE）：对特征含有权重的预测模型(比如简单的线性模型，模型参数就是特征权值向量)，RFE 通过递归减少考察的特征集规模来选择特征。首先，每个特征指定一个权重，预测模型在原始特征上训练，不停迭代优化特征权值，直到那些拥有最小绝对值权重的特征被踢出特征集。如此往复递归，直至剩余的特征数量达到所需的特征数量。

5.2.3 嵌入法（Embedded）

嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于第一种过滤法（Filter），但是是通过训练来确定特征的优劣。

基于正则化。L1 正则方法具有稀疏解的特性，因此天然具备特征选择的特性，但是要注意，L1 没有选到的特征不代表不重要，原因是连个具有高相关性的特征可能只保留了一个，如果要确定哪个特征重要应再通过 L2 正则方法交叉检验。在实际应用中通常会采用带L1的逻辑回归模型+带L2的逻辑回归模型一起来共同筛选。
基于树模型。训练能够对特征打分的预选模型：决策树（Decision Tree）、随机森林（Random Forest）基于树的预测模型。基于树的预测模型的原理就是通过计算特征的重要程序来实现的（《监督学习篇基于树的模型》一文将会详细介绍），所以天然具备特征选择的功能；

参考文献